Objective-Cを知らない子供たち
SwiftがWWDC2014で登場したのは2014年6月2日。OS X YosemiteとXcode 6でSwiftが1.
にもかかわらず、print()の仕様すら変わっています。正直執筆者泣かせもいいところなのですが、
とはいえ、print()すら避けたいので、
実行しないを実行する―遅延評価
で、
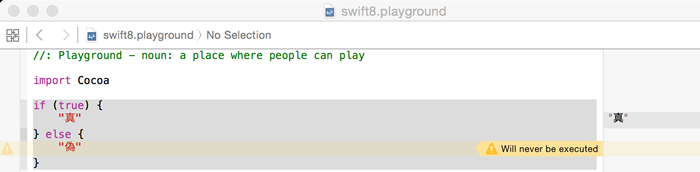
if (true) {
"真"
} else {
"偽"
}なんの変哲もないif文ですが、
それでは、ifなどの構文を使わずに実現できるでしょうか?
次のコードを見てみましょう。
func noop<T>(a:T, b:T){}
var t = 0
var f = 0
noop((t += 1), (f -= 1))
t
f見てのとおり、noopはtもfも0のままのはずですが、tは1に、fは-1になってしまっています。(t += 1)と(f -= 1)が実行されてしまっているのです。
これを防ぐためにはどうしたらよいでしょう?
()を{}に変えてみましょう。つまりnoop((t += 1), (f -= 1))をnoop({t += 1}, {f -= 1})にしてみるのです。今度はどうなったでしょうか? tもfも元のままです。(t += 1)はt += 1を実行した結果」{t += 1}はt += 1を実行する関数」。実行
このことを利用すれば、if文を構文ではなく関数として実装してみましょうか。関数として実装するので、fのように値を返すようにします。
irb(main):001:0> result = if true then "T"
else "F" end
=> "T"
irb(main):002:0> result
=> "T"つまり、? :と同じ機能を持つ関数を実装するのです。ただし、if文も三項演算子も使わずに
import Cocoa
func IF<R>(
PRED:()->Bool, // 引数なしでBoolを返す関数
THEN:()->R, // 引数なし、戻り値Rの関数
ELSE:()->R // 引数なし、戻り値Rの関数
) -> R {
let dict = [ // [Bool:()->()] な辞書
true:THEN, // true には THEN を
false:ELSE // false には ELSE を紐付け
]
let which = dict[PRED()] // PRED()の結果で辞書引き
return which!() // それを実行した結果を返す
}
let truth = IF({true}, {"真"}, {"偽"})
truth
func fact(n:Int) -> Int {
return IF({n <= 1}, {n}, {n * fact(n-1)})
}
fact(10)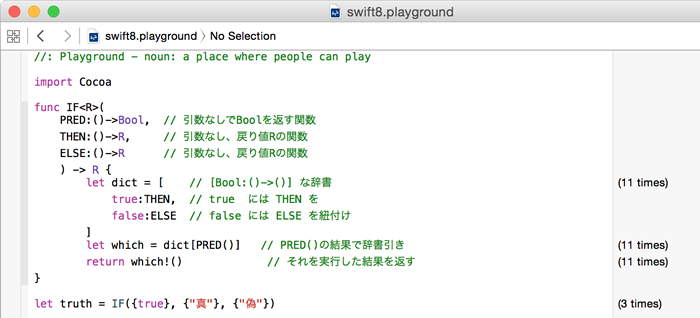
実は同様のコードは連載第1回でも紹介したのですが、IFを実装しています。つまり三項演算子? :と完全に互換です。さらにカスタム演算子の機能を使って任意の三項演算子を定義でき……ればいいのですが、? :しか存在しないのでわざわざカスタム演算子を定義する需要もなさそうなので、
実際Swiftには@autoclosureという属性{}でくくられていることになります。assert()などはそのように実現されているのです。
λはつらいよ
というわけで、
それが関数しかない世界、
この世界において、0や1はどう表現すればよいでしょうか? 結論から言うとこうなります。
func zero<T>(f:(T)->T)->(T)->T {
return {(x:T)->T in x}
}
func one<T> (f:(T)->T)->(T)->T{
return {(x:T)->T in f(x)}
}
func two<T> (f:(T)->T)->(T)->T{
return {(x:T)->T in f(f(x))}
}つまりzeroはfをゼロ回xに適用する関数、oneは1回適用する関数、twoは2回適用する関数というわけです。動的型の関数であればそこで話は終わるのですが、((T->T)->(T)->T、
それではこれを普通の数値にするにはどうすればよいのでしょうか?
こんな感じにすればよいのです。
var n = two({x in x + 1})(0) // 2中身を変えれ、
var s = two({x in x + "*"})("") // "**"これで
/* Operators */
// SUCC := λnfx.f (n f x)
// ((t1 -> t) -> t2 -> t1) -> (t1 -> t) -> t2 -> t
func succ<T1,T,T2>(n:(T1->T)->T2->T1)->(T1->T)->T2->T {
return {(f:T1->T)->T2->T in {(x:T2)->T in f(n(f)(x))}}
}
// ADD := λm n f x. m f (n f x)
// (t2 -> t1 -> t) -> (t2 -> t3 -> t1) -> t2 -> t3 -> t
func add<T2,T1,T,T3>(m:T2->T1->T)->(T2->T3->T1)->T2->T3->T {
return {(n:T2->T3->T1)->T2->T3->T in
{(f:T2)->T3->T in {(x:T3)->T in m(f)(n(f)(x))}}}
}
// MUL := λm n f. m (n f)
// (t1 -> t) -> (t2 -> t1) -> t2 -> t
func mul<T1,T,T2>(m:T1->T)->(T2->T1)->T2->T {
return {(n:T2->T1)->T2->T in {(f:T2)->T in m(n(f))}}
}
// POW
// t1 -> (t1 -> t) -> t
func pow<T1,T>(m:T1)->(T1->T)->T {
return {(n:T1->T)->T in n(m)}
}
// 0
func c0<T>(f:(T)->T)->(T)->T {
return {(x:T)->T in x}
}
// 1
func c1<T>(f:(T)->T)->(T)->T {
// return {(x:T)->T in f(x)}
return {(x:T)->T in succ(c0)(f)(x)}
}
// 2
func c2<T>(f:(T)->T)->(T)->T {
// return {(x:T)->T in f(f(x))}
return {(x:T)->T in succ(c1)(f)(x)}
}
// 3
func c3<T>(f:(T)->T)->(T)->T {
// return {(x:T)->T in f(f(x))}
return {(x:T)->T in add(c1)(c2)(f)(x)}
}
// see if it works
let v = succ(succ(mul(add(c2)(c3))(pow(c2)(c3))))({x in x+1})(0)
v == 42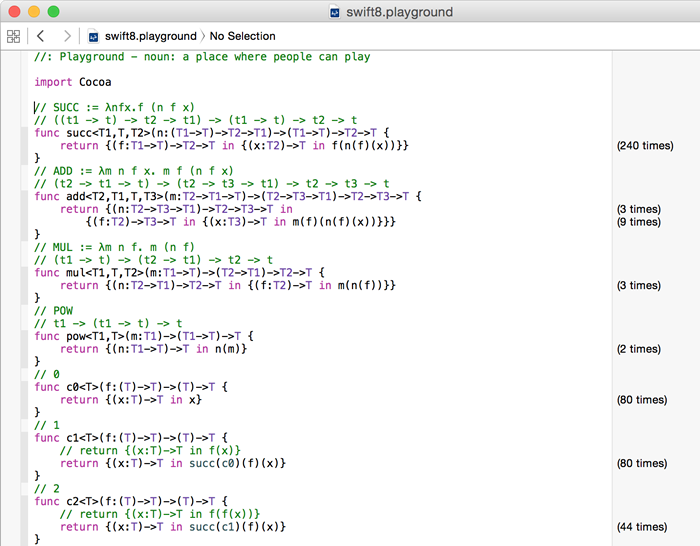
まだSwiftが1になる前に書いたものですが、
次回は……
次回はいよいよSwift 2に触れていきたいと思います。そのときまでに仕様が固まっているといいのですが……。
本誌最新号をチェック!
Software Design 2022年9月号
2022年8月18日発売
B5判/192ページ
定価1,342円
(本体1,220円+税10%)
- 第1特集
MySQL アプリ開発者の必修5科目
不意なトラブルに困らないためのRDB基礎知識 - 第2特集
「知りたい」「使いたい」「発信したい」をかなえる
OSSソースコードリーディングのススメ - 特別企画
企業のシステムを支えるOSとエコシステムの全貌
[特別企画]Red Hat Enterprise Linux 9最新ガイド - 短期連載
今さら聞けないSSH
[前編]リモートログインとコマンドの実行 - 短期連載
MySQLで学ぶ文字コード
[最終回]文字コードのハマりどころTips集 - 短期連載
新生「Ansible」徹底解説
[4]Playbookの実行環境(基礎編)




