前回に引き続きPOP
今回はProtocol-Oriented Programmingが、
PONS=Protocol-Oriented Number Systemの紹介
前回取り上げた実例は、
- 誰かが任意精度の数値ライブラリを用意すれば、
それを使うことも可能
でもそれって本当?
それが、
使い方は簡単。
- ①
git cloneしてPONS.を開いて、xcworkspace Framework-OSXをビルドしたらOSX Playgroundの実例が実際に動くようになります。試しに(1...と打ってみてください。100).reduce(BigInt(1),combine:*) - ②もちろんREPLでも動きます。
make replするとREPLが立ち上がるので、import PONSしてから(1...とか打ってみてください。100).reduce(BigInt(1),combine:*).description - ③読者ご自身のプロジェクトで使いたい場合も、
Frameworkをコピーしてもよし、 ソースファイルをコピーしてもよしです。
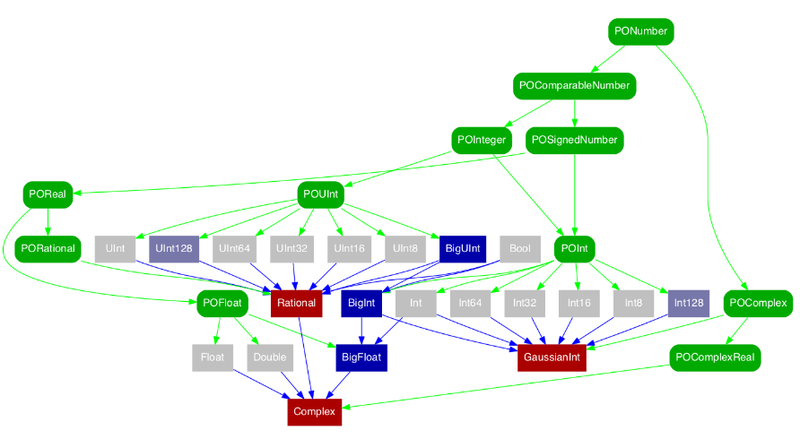
これで、
RubyやPythonやHaskellではおなじみの任意精度整数
( BigInt)が、 GMPなどの外部ライブラリなしで使えるようになります。
→素数判定メソッドも付いてきます。いや、同じく任意精度整数が組込みのPerl6にも組込みだったので。 有理数型
(Rational) もついてきます。分子と分母の型を引数とする総称型ですので、 もちろん任意精度有理数 =Rational<BigInt>も使えます。よく使うのでBigRatととしてtypealiasしてあります。任意精度浮動小数点数
( BigFloat)もついています。 BigRatだけでも好きなだけ小さな数も実現されているのですが、より高速かつ省スペースです。
→総称的に定義された初等関数(elementary functions) の実装も付いてきます。たとえば Float128とか、新たな数値型を実装したときに expやlogやsinやcosを書き直す必要はありません。実際BigRatとBigloatはそれぞれまったく別の型なのに、これらの関数のソースは共通です。
しかし、
1つで十分ですよ、わかってくださいよ!
古のCの時代、man cosしてみると……、
NAME
cos -- cosine function
SYNOPSIS
#include <math.h>
double
cos(double x);
long double
cosl(long double x);
float
cosf(float x);倍精度double用にcos()、float用にcosf()、long double用にcoslと、cosq()でも加えるんですか? 昨今GPUで採用されはじめている半精度cosh()ですか? でも待って、coshはもう双曲線コサイン
ぶっちゃけ付き合ってられませんよね?
Swiftは、
#if os(Linux)
import Glibc
#else
import Darwin
#endifされた状態でXcodeにてcosと打つと……、DoubleもFloatもCGFloatも、cosで呼び出せることがわかります。
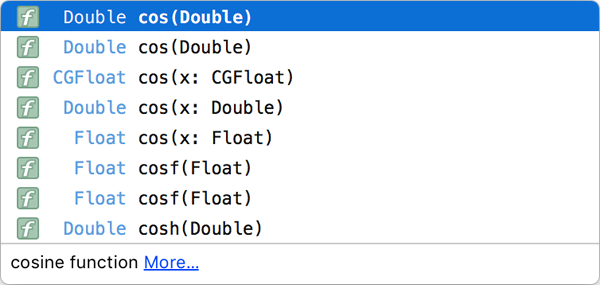
しかし、
こうですか?
func fib(n:Int8)->Int8 { return n < 2 ? i: fib(n-2)+fib(n-1) }
func fib(n:Int16)->Int16 { return n < 2 ? i : fib(n-2)+fib(n-1) }
func fib(n:Int32)->Int32 { return n < 2 ? i : fib(n-2)+fib(n-1) }
func fib(n:Int64)->Int64 { return n < 2 ? i : fib(n-2)+fib(n-1) }だが断る!
だがしかし、
func fib<T>(i:T)->T { return i < 2 ? i :fib(n-2)+fib(n-1) }でもTを足したりTどうしを比較する方法をSwiftは知りませんから、Hogeがあれば、
func fib<T:Hoge>(i:T)->T { return i < 2 ?i : fib(n-2)+fib(n-1) }で行けるはずだ。でもそのHogeってどこにあるの? PONSは、HogeはPOIntegerが相当します。
import PONS
func fib<T:POInteger>(n:T)->T {
if n < T(2) { return n }
var (a, b) = (T(0), T(1))
for _ in 2...n {
(a, b) = (b, a+b)
}
return b
}で、
let F11 = fib(11 as Int8)
let F13 = fib(13 as UInt8)
let F23 = fib(23 as Int16)
let F24 = fib(24 as UInt16)
let F46 = fib(46 as Int32)
let F47 = fib(47 as UInt32)
let F92 = fib(92 as Int64)
let F93 = fib(93 as UInt64)ぜひご自身でご確認を。
しかし、
BigIntでやってみましょう。
let F666 = fib(666 as BigInt)
6859356963880484413875401302176431788073214234535725264860437720157972142108894511264898366145528622543082646626140527097739556699078708088になりましたか?
でも、
……失礼しました。SEGVです。XcodeでProtocolを多様したプログラムを書いていると本当によくお目にかかれます:-(。
しかし数値は整数だけではありません。整数だけで満足できるのは小学生とクロネッカー先生
とはいえこれらを漠然と並べただけでは、
向き合った結果が、
だから、
Double.sqrt(-1) // NaN
Complex.sqrt(-1) // (0.0+1.0.i)
// そもそも比較できない
1.0+0.0.i < 2.0+0.0.i
// 絶対値を見ればおk
(1.0+0.0.i).abs < (2.0+0.0.i).absこれが、
Protocol-Oriented Programming = 正しいものが報われる世界
PONSが目指したもの、intやdoubleの制約を回避するのに涙ぐましいほどの努力をしていて時代を感じさせます。正しい世界とは、
たとえばモンゴメリー乗算というアルゴリズムがあります。これを使うと割り算なしで冪剰余を計算できたりするので素数が捗ったりします。PONSにも実装されているのですが、BigIntがあればBigInt使って」
その一方、BigIntは自分では文字列化メソッドを持っていません。整数の文字列化には、POIntegerでこう実装されています
public func toString(base:Int = 10)-> String {
guard 2 <= base && base <= 36 else {
fatalError("base out of range. \(base) is not within 2...36")
}
var v = self
var digits = [Int]()
repeat {
var r:Int
(v, r) = Self.divmod8(v, Int8(base))
digits.append(r)
} while v != 0
return digits.reverse().map{"\(POUtil.int2char[$0])"}.joinWithSeparator("")元の数を底POIntegerに準拠した数値型は、
そもそもBigIntがあればほかの整数型はいらないという意見もあり得ます。大は小を兼ねるじゃないかという意見もごもっともですが、20! = 2432902008176640000を計算するのに、BigIntではSwift組込みIntのなんと500倍も時間がかかるのです。これはPONSの実装がしょぼいから、Math::BigIntもネイティブな64bit整数の250倍でした。ちなみにPONSのBigIntは世界最速の任意精度整数からはほど遠いのですが、Math::BigIntの5倍の速度が出ています。
コードを使い分けずとも、
PONSでそのことを示せたと自負しています。
予告
実はPONSのようなものは、
I have been working for some time on a rewrite of all the integer types and protocols https://
github. com/ apple/ swift/ blob/ master/ test/ Prototypes/ Integers. swift. gyb. One goal of this effort is to enable operations on mixed integer types, which as you can see is partially completed. In-place arithmetic (anInt32 += aUInt64) is next. Another important goal is to make the integer protocols actually useful for writing generic code, instead of what they are today:implementation artifacts used only for code sharing. As another litmus test of the usefulness of the resulting protocols, the plan is to implement BigInt in terms of the generic operations defined on integers, and make BigInt itself conform to those protocols. 「現在数値型の書き直しに取り組んでいる。その次には
(anInt32 += aUInt64のような) 異なる型通しの演算が控えている。もう1つのゴールは、 整数型プロトコルが総称的なコードを書くのに実際に役立つようにすること。実際にプロトコルに準拠したBigIntを実装するというのは、 そのためのリトマス試験紙となりうる」
Swift 2.
ただし、IntegerTypeとかはそのまま使えませんでした。見てのとおり、ComparableやHashableといった、BigIntでも(1...できるのは、POIntegerがRandomAccessIndexTypeでもあるからです。
次回はそんなsin(1.と書かなくてもsin(1)で型エラーを起こさないかが見えてきます。
本誌最新号をチェック!
Software Design 2022年9月号
2022年8月18日発売
B5判/
定価1,342円
- 第1特集
MySQL アプリ開発者の必修5科目
不意なトラブルに困らないためのRDB基礎知識 - 第2特集
「知りたい」 「使いたい」 「発信したい」 をかなえる
OSSソースコードリーディングのススメ - 特別企画
企業のシステムを支えるOSとエコシステムの全貌
[特別企画] Red Hat Enterprise Linux 9最新ガイド - 短期連載
今さら聞けないSSH
[前編] リモートログインとコマンドの実行 - 短期連載
MySQLで学ぶ文字コード
[最終回] 文字コードのハマりどころTips集 - 短期連載
新生「Ansible」 徹底解説
[4] Playbookの実行環境 (基礎編)




