概要
オイラーの素数の見つけ方は画期的でした。約数の和の漸化式を用いるものだったのです。約数の和が自分自身+1ならばそれは素数です。この漸化式はオイラーの5角数定理によるもので,この定理はガウスやラマヌジャンといった大数学者だけではなく,現代数学にも大きな影響を及ぼしました。本書は,分割数を用いた漸化式,ガウスの3角数,4角数等式などを通して得られるオイラー流の素数の見つけ方などをご紹介します。
こんな方におすすめ
- 高校生,素数・整数・自然数など数に興味を持っている人
- オイラーやガウス,ラマヌジャンが考えたことを知りたい人
目次
はじめに
序章 素数の不思議な見つけ方
1章 「4平方和」と「奇約数和」の不思議な関係
- 1節 ヤコビの4平方定理
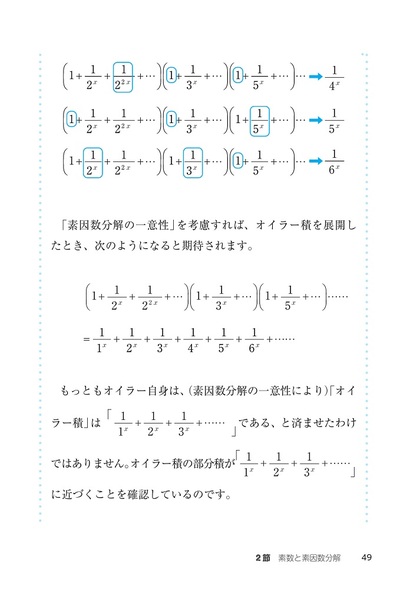
- 2節 素数と素因数分解
- コラムⅠ オイラー積
2章 「分割数」と「約数の和」の不思議な関係
- 3節 整数の分割
- 4節「約数の和」を「分割数」から求める
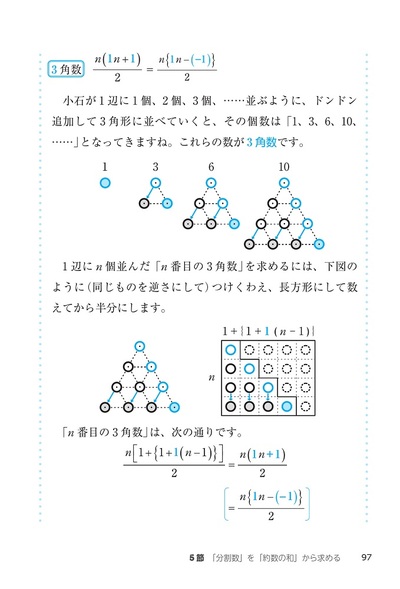
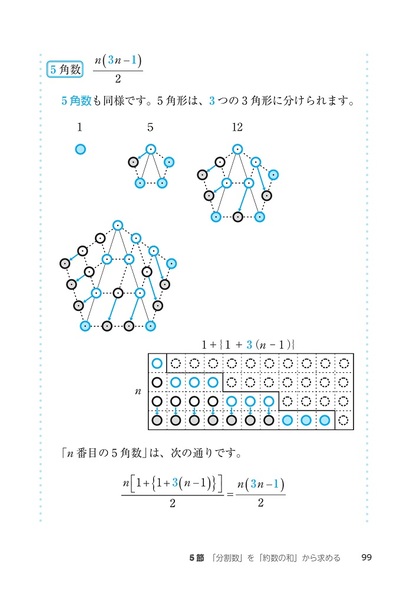
- 5節「分割数」を「約数の和」から求める
- コラムⅡ 多角数(3角数・4角数・……・k角数)
3章 「ガウスの3角数等式・4角数等式」と 「ラマヌジャンの分割数等式」
- 6節 ガウスの3角数等式・4角数等式から「不思議な式」へ
- 7節 ラマヌジャンの分割数等式から「不思議な式」へ
- コラムⅢ 等式「np(n)=knσ(k)p(n-k)」
4章 「ヤコビの3重積」と「6角数等式・8角数等式」
- 8節 ヤコビの3重積公式
- 9節 6角数等式・8角数等式から「不思議な式」へ
- コラムⅣ ヤコビの3重積とテータ関数
5章 もう1つの「多角数等式」
- 10節 もう1つの多角数等式から「不思議な式」へ
- コラムⅤ sinxとϑ3(v,τ)(3 角関数とテータ関数)
特別寄稿 久保田富雄(著)
サポート
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
上から3行目の式
| 誤 |

|
|---|
| 正 |

|
|---|
上から4行目の式
| 誤 |

|
|---|
| 正 |

|
|---|
上から7行目の式の2項目
| 誤 |

|
|---|
| 正 |

|
|---|