補足情報

特集3「［速習］統計分析──メジャーリーグのデータで学ぶ」

一部紙幅の都合上掲載できなかった解説がありますので、こちらに掲載します。

相関行列

複数の数値の相関を一気に出す

なお、相関関係を分析する際、どの数字とどの数字の相関をとるかは、経験則による仮説などさまざまな要素をヒントに考えていくことになりますが、切り口が見えてこない場合もあります。分析のきっかけとして関連する数字の相関を一気にとる方法があり、分析の糸口をつかむのに便利なので紹介します。それは、相関行列を作るという方法です。

打撃成績であれば、安打、四球、本塁打、三振、盗塁など多くの項目が並んでおり、そこから計算できる指標も打率、出塁率、ISOなど多数考えられます。このとき「どれかとどれかに意外な相関関係にあったりするのではないか」と考えてみても、相関関係を分析する組み合わせは可能性としては「安打と四球」「四球と本塁打」「安打と本塁打」「四球と盗塁」……というように膨大であり、一つ一つ散布図を作って決定係数を出すのは面倒です。

相関行列の作成

こういった場合に、いちいちそれぞれの相関をとるのではなく、考えられる組み合わせの相関を一気に測ろうというのが相関行列の考え方です。詳しく理解するためには実際に見たほうが早いので、表を作成してみます。

付属データの「4-3 相関行列元データ」のシートにチーム打撃成績が入力されていますので、［データ］タブから［データ分析］アドインを立ち上げ、［相関］を選択して［OK］を押します。［入力範囲］は得点以降のすべてのデータを含む「$D$1:$W$421」とし、［先頭行をラベルとして使用］のチェックをオンにして［OK］をクリックします。そうすると図1の相関行列が出力されます。

図1　相関行列

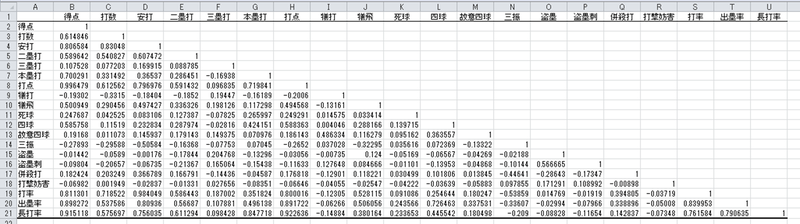
ここでは「相関係数」という数字が計算されています。相関係数は決定係数と同じように相関関係の強さを表す指標で、完全な負の相関関係から完全な正の相関関係までを-1～+1の数値で表すものです。0のときは無相関です。相関係数を2乗すると決定係数になるという関係があります。

相関行列では、たとえば得点の列・打率の行を見ると0.811301であり、得点と打率に正の相関関係があることがわかります。またその下には出塁率もあり、0.898272となっていることから出塁率のほうが相関関係が強いことが即座に確認できます。