11月28日、ベルサール汐留にて、FITC Tokyo 2009が開催された。以下は、Mario Klingemann氏のセッションのレポート。

Mario Klingemann氏「Connectiong the Dots」

Quasimondoの愛称と、特徴的な 角の生えた"Q"のマークで有名なMario Klingemann（マリオ・クリンゲマン）氏は、氏自身の作品が芸術展に出品されるなど、国際的に評価されるネットアートの代表者として名高い。

「在学中数学は好きでしたか？」とマリオ氏が問いかけると、会場から思いのほか手が上がったのか、おどろいた様子で「Oh My God！」と叫んだ。マリオ氏曰く、普通はNoと答えるのが98.2％で残りの0.2％が好きとのことで、氏自身も在学中には「実際の生活には全く役に立たないもの」と思っていたという。しかし、プログラミングとアニメーションと出会ったことで、数式を覚え、「⁠なるほど、こういうところで数学は役に立つんだな」と学んだと語る。それからは数学の本を読み始め、どんどん数学の魅力に取り憑かれていったそうだ。

スライドにActionScriptで表された数式が表示された。そして、「⁠さきほどキース氏の発表で、さまざまな数式が紹介されたと思うが、私が好きなのは純粋な数学」と述べ、自身が数式への興味よりも、そのものの概念を見いだすことに魅力を感じると語った。氏によれば、"数学の概念・パターンから究極の美を見つけること"が好きだとし、「⁠さまざまな科学の中で、ひとつの真実をみつけたら、永遠に変わらないのは数学だけ」と数学に対する思いを述べた。

芸術と数学には共通点がある。例えば、芸術家は筆を使い、数学者は数を使う。また絵筆を使うことは、計算ができることに相当し、芸術家は美を求める為に何年も書き続けるが、数学者は証明するために何年も書き続けるという。そのような情熱をもって取り組むという意味でも共通していると氏は述べる。

マリオ氏は『素数の音楽』という本について紹介した。素数はそれ自身、もしくは1でしか割り切れない数のことで、非常に魅力があるテーマだという。「⁠素数を算出できる式を、数学者は何百年もかけて導くことができないか探してきた」とし、自身でも挑戦してみることにしたという。そこで、出会ったのが「Ulam Spiral」だった。Ulam Spiralは、1、2、3、4、5、...と、数を四角螺旋状に配置していき、素数だけをハイライトしていくというもの。それを繰返していくと、法則性を持ったパターンが生まれる。氏は、こういったスパイラルやパターンはもっと他にあり、そこから別の答えが導き出せるのではないかとし、別のアプローチでパターンを作ろうと思うに至ったそうだ。また、別の本『Mathographics』を読んでいたところ、この本には円形螺旋状のスパイラル・パターンが載っていたという。そこで、これを素数に当てはめて、Flashでつくってみたところ、大変おもしろい結果になり、明確な形が見えてきた。

これを得て、マリオ氏は"凄い発見"をした、"歴史に名を残せるのではないか"と考えたが、これは既に発見されたSacks Spiralと呼ばれるものだった。だが、氏は諦めなかった。この間にも様々な形で試行錯誤を繰返し、今度はある古本屋で見つけた『Connections』という本に、フィボナッチ数に関する記述が見られたため、これをスパイラルに適応したところ、ある因子が入力されたとき、素数のラインが放射状に一直線になるという現象を発見する。このとき、ラインにのっているのは、すべて13で終る素数だった。そこで何かを導き出せたわけではないが、その時の因子が2.4137903555081だったことで、これが一体何を意味するのか考えるようになったそうだ。まずは、この数が何を意味するのかを、数学専用の検索エンジンWolframAlphaで調べた。氏は、その結果に"魔法のにおい"がしたという。そこで考えを巡らしたところある式を導きだしたが、結局そこから何も得ることは出来なかったと述べた。だが、意味をなさなくても、結果が出なくても、充分満足したと語る。

圧縮についても解説があった。マリオ氏は"数学的に興味深い概念"とし、「⁠大量のデータを特定のルールで整理し、データとルールとを乖離させることでデータに必要な容量を減らす非常にエキサイティングな分野だ」と説明。また、圧縮は制約されたリソースやスペースをいかに活用するかが難しいが、「⁠制約があるからこそ、クリエイティビティが生まれる」と語り、圧縮にも情熱を傾けていることをうかがわせた。ある日、マリオ氏はTwitterでPapervision3Dの開発者の一人としても知られる、Ralph Hauwert（ラルフ・ハワート）氏からのつぶやきで、意味不明な暗号を受け取ったという。最初は何を意味しているか理解しがたかったが、次のつぶやきで、それが画像をTwitterの140文字に合わせて暗号化したものだとわかると、"競争心がかき立てられ"、ラルフ氏と画像圧縮競争をすることになったという。そこでマリオ氏はさっそく作業に取りかかり、世界でも有名なモナリザを圧縮することに決める（欧米のプログラミング文化では、モナリザがサンプルとして非常によく使われている⁠）⁠。

140文字という限られた制限で圧縮するわけだが、そもそも文字（キャラクター）とは、アスキーコードで表現され、値として0-255が設定される。ところが最初の0-31までは、コントロールキャラクター（EOTやBSなど、システムに深く関わるキャラクター）のため使うことができない。そこで、安全なBase64を使用し、かつ仕掛けを施すことで、あらゆる値をBase64に変換することにした。しかし、Base64にしてしまったことで別の問題も浮上してしまった。Base64にエンコードするために、33％あまりの容量を余分に消費してしまうことになったのだ。これによって、140文字をBase64に変換した場合には102byteしかおくることができず、結果的に9*11ピクセルという、到底モナリザにはみえない画像になってしまうことが明らかになってしまった。また壁にぶつかってしまった氏だが、諦めることなく、今度はUTF-8につかう事を検討した。なぜならTwitterでは、140文字という制限を掛けながらも、マルチバイトに対応するためにUTF-8を使っているからだ。UTF-8は、現状の定義では一文字を最大4バイトまでの可変長の数値に変換する。これを利用することで、最大210byteまで使用することができるようになり、より多くの情報をTwitterでつぶやけるわけだが、これでも17*12ピクセルで、モナリザにはちょっと見え辛かったようだ。それでも、氏は諦めない。そうして出た結論。それは、そもそもピクセルグリッドで表現するのをやめたらよいのではないかという答えだった。

そこで氏が目を付けたのが、ボロノイ図だった。ボロノイ図は、複数個の点によって表現され、点と点との距離領域分けされている。こちらのほうがピクセルを敷き詰めて使うよりも情報量は少なくて済むはずと考えたのだ。ところが、必要な情報量の割り出しで問題が発生する。XY座標に必要な浮動小数値（float）が8byte,そしてカラーを表現する24bitRGBで3byteが必要になり、ひとつのポイントで合計11byteの情報量が必要になる。ということはつまり、210byteの制限で19ポイントしか打てない事になってしまい、これではピクセルよりも出来が悪くなってしまう。氏はこれを必要最低限な情報だけにとどめることで解決した。まず、座標の精度を下げ、XYそれぞれ1byteずつ、幅と高さをパーセンテージ（0-100）として表現し、さらにカラーを8色にまで下げ、カラーテーブルに頼ることで実際に格納する情報をカラーテーブルのインデックスのみの1Byte（実質3bit⁠）⁠、合計3byteに抑えた。これによって、必要な情報量は、全体に必要なカラーテーブルの24byteと、座標とカラーインデックスの3byteとなり、62ポイントまで増加させることに成功した。それだけではない。前述のとおり8色のカラーインデックスを格納するのに必要なのは3bitだけのため、残り5bitを無駄にしてしまう。そこで、さらに3bitをカラーインデックスに回し、あとの2bitをブレンドさせるための因子とすることで、階調表現が可能になったと説明した。

次にマリオ氏は、モナリザとなり得るための座標とカラーインデックスの取得に、遺伝的アルゴリズムを用いたと紹介。遺伝的アルゴリズムに関する詳しい解説はここでは省くが、ある因子を親として新しい因子を生み出し、それが親よりもよい結果ならば、そこから新しい因子を生み出し、悪い結果であったなら変異を起こした因子を生み出すといったサイクルを起こすことで、最終的に最善の方向を探索し、モナリザに近づいていくというのだ。氏は、その様子を実際に紹介した。

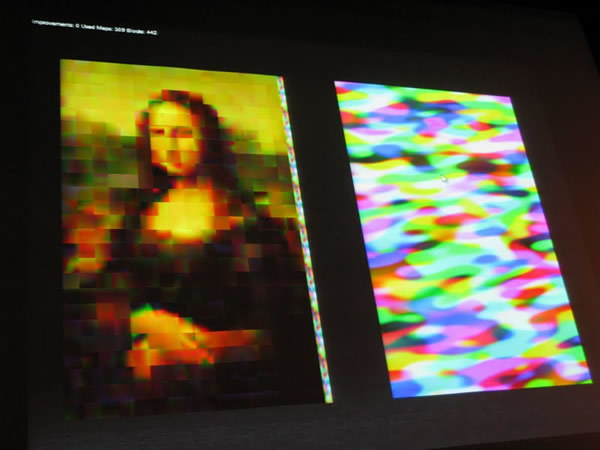
真ん中が対象となる画像（モナリザ）であり、左が遺伝的アルゴリズムによって導かれた結果のボロノイ図、そして右が結果と対象の比較である。この比較では、暗い部分がより対象に近づいている部分だという。この最終的な結果はflickrにアップロードされている。この画像は世界中で話題を呼び、20万人のアクセスがあったとした。

「この経験で私は、画像の再構成についてもっと探求したくなった」と氏は語っている。

そしてマリオ氏が着目したのは、疑似乱数を使ったアプローチ。疑似乱数を元にタイルを作り、個々のタイルと元の画像のタイルの位置とを比較し、その違いを計算していき、違いが少ない場合、それを維持していくような形をとった。ここで使われたのが、ActionScriptのPerlinNoizeだ。対象となる画像（モナリザ）を、PerlinNoizeで生成されたビットマップのタイルとを比べ、モナリザを再構成していく。

しかし、問題はPerlinNozeの生成に非常に時間が掛かることだと氏は述べ、次にノイズ画像をタイルとして生成することにし、若干のスピードと質の向上が見られたとした。

とはいえ、「⁠まだ完璧とはいえない」と氏は語る。この結果から、モザイク画像のインスピレーションを受け、今度はノイズではなくモナリザではない他の画像をタイルとして生成するとどうなるかという実験をしたという。

するとかなりのスピード向上が見られ、かなりおもしろい結果が見られたと述べた。そしてここから、グリッドに違和感を感じだし、前述でも登場した"ボロノイ図"を活用。マリオ氏自身（quasimondo）のロゴを対象として実験したスライドを公開した。

また、対象のディティールの細かいところは、比較するボロノイ図のパターンの領域も細かく、大ざっぱなところは大きく捉えるというサンプルを作成。そのディティールについてはエッジから判断し、エッジが多いものは情報量が多いとしながらも、多すぎるものはノイズになってしまうため、多すぎず少なすぎずのその中間領域を見つけていくとした。そしてDisplacementMapFilterをかけることで、境界がなじみ、より有機的になると解説。これらの手法とマリオ氏自身が撮影したテクスチャを使って生成された作品が紹介された。

最後に、このプロジェクトを進め、現在ツールの制作と公開を検討しているというマリオ氏。今から楽しみである。

マリオ氏は語る。「⁠数学を見直して欲しい。数学にはいろんな宝がかくされている」と。実際、このセッションは非常にレベルが高く、ネットでも日本の多くのトップレベルFlash開発者に高評価を得ていた。著者自身、このような貴重なセッションを聞けたことを大変光栄であり、またとないチャンスだったと思う。そう、マリオ氏が語ったように、このセッションを見た来場者の多くは、数学を見直したことは間違いないだろう。そして、その宝をマリオ氏自身が分配したに他ならない。あなたも、是非休日、数学に思いを巡らせて欲しいと思う。素晴らしいセッションだった。