【特別寄稿】今すぐ役立つ！文系のための数学的発想講座 ──演繹法と帰納法

――ぶれのない論理力を身につけて的確に仕事をこなしたい…、そんなビジネスパーソンはけっこう多いはず。そこで『大人のための数学勉強法』（⁠ダイヤモンド社）などの著書を持ち、NHK（Eテレ）『⁠テストの花道』に出演するなど話題の「大人の数学塾」塾長、永野裕之さんにご登場いただき、“⁠根っからの文系⁠”こそ今すぐ使える数学発想術について語っていただきました。

はじめまして。私は永野数学塾（大人の数学塾）塾長の永野裕之と申します。この度、技術評論社さんで『根っからの文系のためのシンプル数学発想術』を上梓させていただいた関係で、当記事を担当させていただくことになりました。どうぞよろしくお願いいたします。

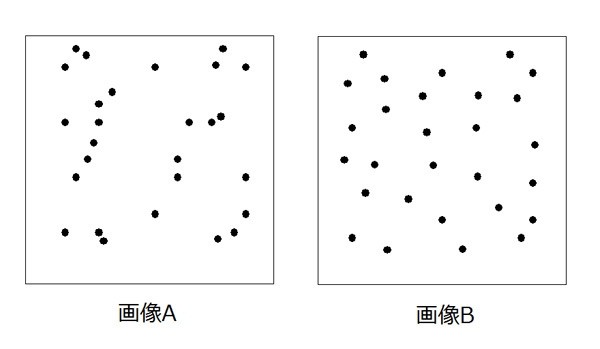
ところで…いきなりですが問題です(・_・;)

［問題］下の画像を見てください。片方は雨が道に落ちたときの様子を記録したもので、他方は人為的に作ったものです。雨が道に落ちたときの様子を記録したのはどちらでしょうか？

「そりゃあBでしょう」

と思った人が多いと思いますが、実は雨が道に落ちたときの様子を記録したのは画像Aです。均一なものはランダムで不均一なものには意味（作為）があると思うのは単なる人間の思い込みに過ぎません。

ただし、

「こういうのはだいたい引っ掛けだよ。Bだと思わせといてAでしょ」

と思った人にも、鋭い読みではありますが論理的には正解をあげることはできません。雨が道に落ちるとき、画像Aのようになることも画像Bのようになることも両方あり得るからです。この問題には画像Aを正解とする根拠もありませんので、論理的に考えれば正解は「わからない」になります。

意地の悪い問題でごめんなさい。直感はアテにならないことを実感してもらうための問題でしたm(_ _)m

数学力とは何か？

ではこのような直感が通用しない問題に直面したとき、私たちは何を頼ればいいのでしょうか？ そんな時こそ、数学力の出番です。

あ、今、

「僕は（私は）文系だからどうせ無理だよ…」

と思ったあなた、ちょっと待ってください！「⁠数学」と言っても、2次方程式や三角関数が必要なわけではありません。これらは忘れてしまっても何ら問題ないのでどうぞご安心を(^_-)-☆

ここで私が事あるごとに引用させてもらっているアインシュタインの言葉を紹介しましょう。

「教育とは学校で習ったすべてのことを忘れてしまった後になお、自分の中に残るものをいう。そして、その力を社会が直面する諸問題の解決に役立たせるべく、自ら考え行動できる人間をつくることである」

─⁠─アインシュタイン

数学力の本当の姿もこの言葉に集約されています。中・高の数学に出てくる関数、方程式、ベクトル、数列等々は、論理力を磨くための道具に過ぎません。公式を覚えていることも、解法をたくさん知っていることも、数学力とは何ら関係がないのです。それらを全て忘れてしまってもなお残る、問題解決のためのアプローチの方法、その発想術こそ数学力の本当の姿であると言えるでしょう。

そしてそれは、あなたが「根っからの文系」だったとしても決して無理な発想術ではありません。いや、むしろ「文系」であるあなたこそ大きな可能性を秘めています！(｀･ω･´)ゞ

国語力こそ数学力の源

私の塾で短期間に数学の成績を伸ばす生徒さんに共通しているのは、数学が苦手でも国語は得意だという点です。文章を読んだり書いたりすることが得意な生徒さんは、（⁠本人は気づいていなくても）すでに論理的にものごとを考えるための下地が十分にできあがっているので、ちょっとしたきっかけを与えるとあっという間に数学の力を伸ばします。そういうケースは跡を絶ちません。私はいつしか「国語力こそ数学力の源である」が持論になりました。

拙書『根っからの文系のためのシンプル数学発想術』は、文系の人が元来持っている数学の力、数学的発想力を呼び覚ますための本です。

数学発想術～7つのパターン

私が拙書の中でご紹介した7つの発想術は以下の通りです。

① 整理する
② 順序を守る
③ 変換する
④ 抽象化する
⑤ 具体化する
⑥ 逆の視点を持つ
⑦ 数学的美的センスを磨く

いかがでしょうか？

少なくともいくつかは

「あ、こういう考え方なら普段から使っているかも」

と思ってもらえるのではないでしょうか？

数学は「才能」のある人だけの専売特許ではありません。数学的に発想することは誰にでもできることなのです。というより、多くの人はすでに無意識のうちに数学的に発想しています。

ただし意識してそれができるかどうかは大きな違いです。意識していないと「ヒラメキ」（⁠と感じることでしょう）に頼らないと問題が解決できなかったり、良いアイディアが浮かばなかったりしますが、数学的に発想するということが、どういうことかがわかっていて、それを意識することができれば、問題を解決することも、他人には斬新に思えるアイディアを手に入れることも必然的にできるようになります。同時にあなたの言葉は大いなる説得力をもって人の耳に響くようにもなるでしょう。

どうぞ詳しくは拙書をご覧ください……ではあんまりなので、ここでは上記数学発想術のパターン⑤「具体化する」で取り上げた「演繹法と帰納法」の項をご紹介したいと思います。

演繹法と帰納法

演繹法と帰納法はどちらも、論理的に既知の事柄から未知の事柄が正しいことを導こうとする推論の方法ですが、そのアプローチの仕方は正反対です。

演繹法: 「全体に成り立つ理論（仮定）を部分にあてはめていくこと」
帰納法: 「部分に成り立つ理論（仮定）を全体にあてはめていくこと」

たとえば、目の前に美しい桜が咲いているとき、

「桜の花は散る。だから、この桜もいつかは散ってしまうだろう。」

と推論するのは演繹的な考え方です。

「去年も一昨年もその前の年も桜は散ってしまった。だから桜は必ず散るだろう」

と推論するのは帰納的な考え方です。

いかがでしょうか？普段、演繹とか帰納とかいうことは意識しないかもしれませんが、どちらも日常生活で皆さんが普通に使っている考え方だと思います。もう少し他の例も出しますね。学生時代、学校にいつも難しいテストを作る先生が一人はいたでしょう？仮にA先生がそういう先生だとします。

「ああ～明日はA先生のテストかあ。また難しいんだろうなあ」

と考えるのは演繹的です。ここで「A先生のテストはいつも難しい」というのはA先生のすべてのテストに共通する性質が抽象化されています。対して「明日のテストが難しい」というのは具体例ですね。このように演繹法というのは、抽象化された事柄を具体例にあてはめることを言います。

一方、A先生が新任の先生だった場合に、

「一学期も二学期も三学期もA先生のテストは難しかったなあ。A先生というのは難しいテストを作る先生なんだ（後輩にも教えてあげよう⁠）⁠。」

なんて考えるのは帰納的です。ここで「一学期も二学期も三学期もA先生のテストは難しかった」というのはそれぞれ具体例になっていますね。対して「A先生のテストは難しい」というのはA先生のテストに共通する性質を抽出していますから抽象化です。つまり帰納法というのは、具体例からそれぞれに共通する性質を抜き出して抽象化することです。

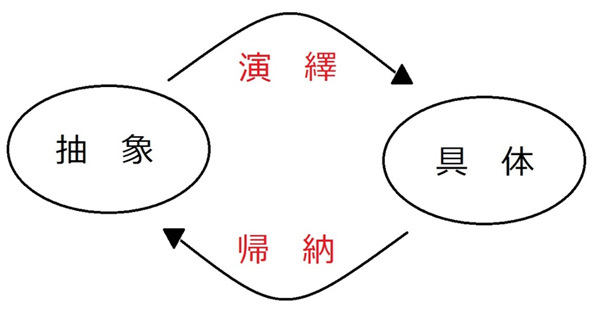
以上をまとめますと、次のように図式化することができます。

…と、ここまで読んでくれたあなたは、

「わかるけど、どこが数学なの？」

と思うかもしれないですね。

数学（算数）ではこんな風に、演繹と帰納を使い分けてきました。

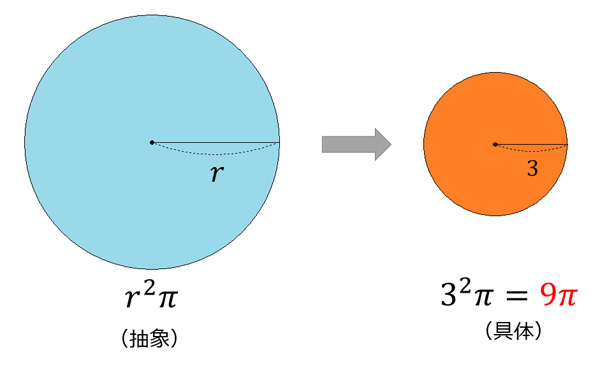
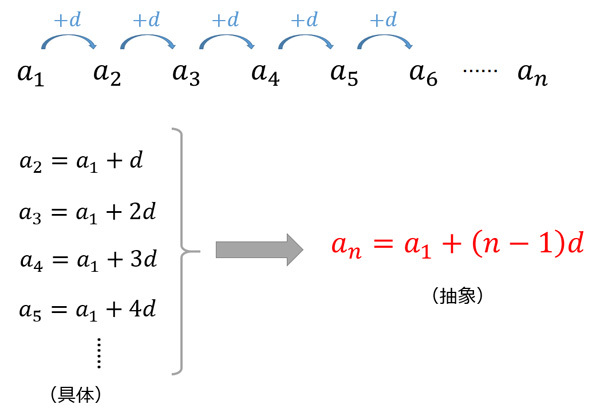
演繹と帰納の使い分け

演繹と帰納についてはわかりましたね？(^_-)-☆

ではこの2つの推論の方法をどのように使い分けていけば良いのでしょうか？こんな例で考えてみましょう。ある文房具メーカが新製品の開発を行うとします。およそ次のような段階を経ると思います。

①調査→②企画→③設計→④試作→⑤営業

①調査

売れ筋の商品を調査し、ターゲットとする客層に対するアンケート等を行います。どのような商品について調査をし、どのような項目についてアンケートを取るかを具体的に決めていくのは演繹的です。次に具体的なデータが得られたら、ヒットしている商品に共通するデザイン・性能・価格などを、統計処理等を利用しながら抽象化しますので、今度は帰納的な手法が必要になります。

②企画

①の結果を元に新製品のアイディアを練ります。①でヒットしそうな商品のスペックはすでに抽象化されているので、今度はそこから具体的な新商品を考えていきます。今度は抽象→具体なので演繹的手法です。

③設計

既存の技術と新技術の組み合わせで最良の方法を模索します。すでに「◯◯が作れる」と理論化（確立）されている新旧の技術を具体的に新製品に使っていきます。すなわち演繹的です。

④試作

試作品が出来上がったら、使用実験・顧客モニター調査などから設計の問題点と改善点を明らかにします。①と同じように実験方法や調査項目の選定は演繹的に行い、得られた具体的なデータは帰納的にまとめていきます。

⑤営業

試作の問題点が解消されて、晴れて製品化された後は、これを売るためにプレゼンテーションしていきます。営業にも演繹と帰納の考え方を応用するために少し拡大解釈をして新製品の「売り」をいくつかの特徴から抽象化された「結論」と考えます。「⁠売り」に強烈なインパクトがある場合は、演繹的に提案していくのが良いかもしれません。たとえば「今度の我が社のボールペンは、インクが永久に切れないんです！」とインパクトの大きい結論（売り）を先に言うと、先方は「え～～！なになにどういうこと？」と食いついてきてくれるでしょう。その後で「と言いますのは…」と具体的な話を進めれば、最後まで興味深く話を聞いてくれるはずです。

反対にインパクトがそう強くない場合、最初に「今度の我が社のボールペンは、価格が当社比で10％減の90円なんです」と言っても、「⁠ふーん」とあまり積極的には聞いてもらえないかもしれません。そのような場合は「先日発売されたA社のボールペンは100円です。同じく新発売のB社のものは、A社よりも書き味が優れていて価格は110円です。一方当社はB社よりもさらに書き味の良いものを開発いたしました。」と先に具体的な話をしましょう。

その後で「しかも価格は90円なんです！」と続ければ、B社よりも高性能ならもっと高いんだろうなあと予想していた先方は意外に思って興味を持ってくれることでしょう。具体例から初めて最後に一番言いたい結論（売り）をもってくる帰納的な手法を使うことで、インパクトの弱さはカバーすることができます。

いかがでしょうか？最後の営業に関しては、推論ではないので演繹や帰納といった言葉を使うのは厳密には不適切ですが「結論（抽象⁠）⁠→具体」を演繹、「⁠具体→結論（抽象⁠）⁠」を帰納と解釈することで、演繹や帰納といった思考法が応用できる場面を拡大しています。

アンケートひとつを取っても、項目の選定は演繹的で、得られたデータをまとめるのは帰納的な思考です。このように演繹と帰納は組み合わせて使うことで大変大きな力を発揮します。演繹と帰納の使い分けが意識できるようになると今までは無意識だった思考プロセスが明確になり、アイディアを練ったり、マーケティングを行ったりする際にきっと役立ちます！

上記は『根っからの文系のためのシンプル数学発想術』のほんの一部です。ご興味を持たれた方はぜひ、手に取ってみてください。m(_ _)m