本書(ピタゴラスの定理でわかる相対性理論)p.65-66では、球面三角形の面積について解説を行ったのですが、じつは紹介仕切れなかったことでとても面白い話があり、今月はその話をしてみたいと思います。
球面三角形の面積を求めるものに、本書で紹介した「ガウス・ボンネの定理」があります。実は、この定理の式から、面白いことに、皆さんご存知の平面幾何の「三角形の面積」を求める式を導くプロセスを紹介しましょう。そして皆さんからより良い証明ができれば是非教えてほしいと思います。では試みてみます。
球面三角形の面積はガウス・ボンネの定理は、
によって与えられる。ここでは内角をα、β、γの代わりにA, B, Cとしている。
図1 球面上の小さな三角形
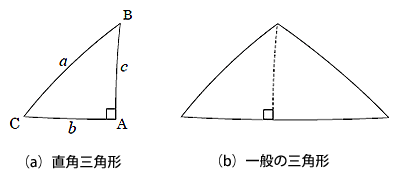
三角形が小さいときには平面三角形の底辺×高さ÷2になることを証明する道筋を紹介しよう。
まず、余弦定理として本書p.66の(3.5)のほかにもう一つ補完的な定理がある。それは角と辺に関するもので次式である。
cosA = -cosB・cosC+sinB・sinC・cos(a) ……(2)
これはさらに次式になる。
cosA = -cosB・cosC+sinB・sinC・cos(a) ……(3)
ここで図1のように∠Aが直角の場合を考えることにしよう。一般の三角形は図(b)のように2つの直角三角形に分解して扱えばよい。つまりここでは、辺a、b、cが1に比べてかなり小さいときには三角形の面積がbc/2になることを説明すればよい。
∠Aが直角のときには(3)式の左辺が0となるので次式がえられる。
cos(B+C) = -2sinB・sinC・sin2(a/2) ……(4)
(1)式において∠Aを直角(π/2)とすると
となるが、三角形の形が小さいときにはB+Cがπ/2よりも僅かに大きい程度であり、括弧の中は1に比べるとかなり小さい。このときには次の式の近似が許される。
B+C-π/2 ≈ sin(B+C-π/2) = -cos(B+C) ……(6)
さらに(4)を使って次式を得る。
B+C-π/2 ≈ 2sinB・sinC・sin2(a/2) ……(7)
さらにここではaが1に比べて十分に小さいのでsin(a/2)≅a/2であるから、これは次式となる。
B+C-π/2 ≈ (a2sinB・sinC)/2 ……(8)
よって面積は
S ≈ (a2R2sinB・sinC)/2 ……(9)
となるが、ここで
b =aRsinB
c =aRsinC ……(10)
であるから、結局
となる。このように、小さな三角形に対しては、(1)式から底辺(b)×高さ(c)÷2が導かれる。



