光とはなんぞや、光の数式表現に挑戦
『ピタゴラスの定理でわかる相対性理論』の第7章は、本書のクライマックスです。第6章まではユークリッド幾何を超えて創られた双曲幾何が、人工的なものにも思えたのですが、第7章ではこの宇宙を支配する時間を含めた4次元空間に、双曲幾何が潜んでいることを明らかにしています。そして第7章の物語の主役は、アインシュタインです。
1895年、彼が16歳のときにアーラウで得た疑問は、次のようなものでした。
「もし光速度で光の波を追いかけたら、光の波は静止して見えるだろうか。まさかそのようなことが起きるとは思えない。」
1887年にマイケルソンとモーレイの実験によって、光の波の速度は、観測者の速度によらないで、一定の秒速30万キロメートルであることが判明していました。
それ以前の1864年には、マックスウェルは電磁波の存在を予想したばかりでなく、その伝播速度の計算結果があまりにも光の速度に近いことから、1871年にはまだ発見されていなかった電磁波は、光と基本的に同じものだと主張しています。
今日では、光は周波数の大変に高く波長の短い電磁波だということはよく知られています。可視光は、波長で1ミクロン(千分の1ミリメートル)より短い0.35~0.8ミクロンの範囲です。あとで実験を語る電磁波の波長は、ほぼ100メートルです。
ヘルツが電磁波を実験で実証したのは、1888年です。20世紀が明けて1905年、アインシュタインが、光速不変を公理とした新しい物理学の基本を示しました。それが相対性理論です。
今回は電磁波とそれに関係する基本的な数学表現について、身近な電線を取り上げて語ってみようと思います。
相対性理論の多くの本には、光とは何ぞやという基本的な問題をあまり書いていないのですが、それは使う数学が高度になることが要因かと思います。苦言になるのですが、数学をきちんと使いこなして読者を説得させるという著者の技量が足らないように思われます。
『ピタゴラスの定理でわかる相対性理論』では、あえて難しそうな数式を幾何学のために使ってみたのですが、分かりやすく噛み砕く工夫は怠りませんでした。そのことに満足を感じてくださった読者が多いようです。それでも、微分や積分は使いませんでした。
ここでは微分、しかも偏微分というものをあえて使うことにしますが、詳しい説明は割愛します。理系ですと大学1~2年の科目だからですし、高校の学ぶ微分の延長に過ぎないからです。
波の動きを表現する
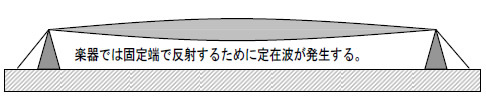
波動を目に見える形で表すには、図1のような楽器の弦があります。弦の長さが比較的短くて2つの端が固定されている状況では、指ではじくと定在波がおき、これが空気に伝播して音として聞こえます。
図1 弦に発生する定在波
長い弦を想定してその一部を、例えば図2のような山形にして解き放つと、山の高さが半分ずつのになった形が、右と左に伝播します。これが基本的な波動です。
図2 弦に伝播する波動
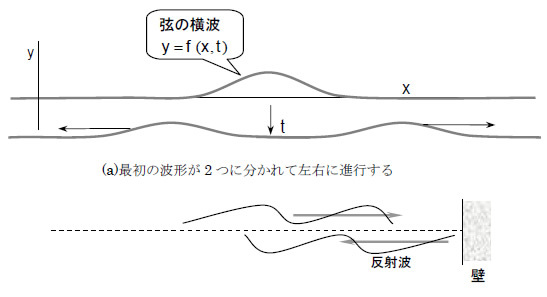 (b)弦に伝播する非分散性波動は左右に形を変えないで進行し、固定端で裏返って反射する。音波は壁で反射する。
(b)弦に伝播する非分散性波動は左右に形を変えないで進行し、固定端で裏返って反射する。音波は壁で反射する。
この波動の挙動を支配する微分方程式は、次のようなものです。

ただし、y=弦の変位、 σ=弦の単位長さあたり密度、T=弦の張力です。
このように、ある物理量の時間の2階微分と空間の2階微分が正の比例関係になるとき、比例係数の平方根が、波動の伝播速度vになります。

仮に、1mあたり1g(=0.001kg)の弦に、10キログラム(98.7ニュートン)の重量の錘をつるした場合に相当する伝播速度は316m/sです。光速に比べて、ほぼ百万分の1の速度です。
弦の両端が固定されていると、そこで反射が起き波が跳ね返り、左右に行き交う波動が重なりによって定在波になります。音波の場合には、壁が硬いとそこで跳ね返って残響となります。また壁がやわらかいと、吸収されてこだまが無いので残響がありません。
平行フィーダー線を伝わる電磁波の速度を表す
アンテナで受信した電気信号をテレビにもってくるのに、図3のような平行フィーダ線というものがあります。筆者はこの記事の実験のためにホームセンターで買いもとめました。
図3 電磁波を誘導するケーブル
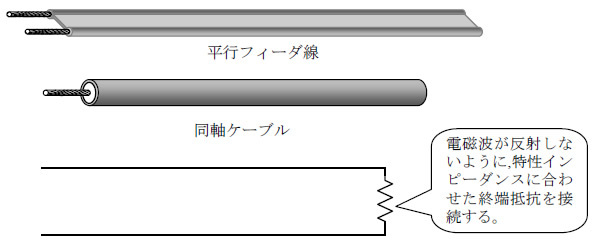
フィーダ線は、電磁波をこの電線に沿って伝播する仕掛けの一種です。端の2本の端子を解放しておくと、それは弦でいうと固定端のようなもので、電磁波が反射して左右を往来します。
しかし適当な抵抗で端を接続すると、あたかも無限に平行フィーダが伸びているかのようになり、反射がなくなります。その抵抗値を特性インピーダンスといいます。平行線の場合、特性インピーダンスは300Ωのものと200Ωのものがあります。
このようにした実験装置で、入力端にパルス状あるいは波束の電圧信号を与えると、フィーダ線の周辺に電磁波が形成されて、それが出力端に向かって伝播するのです。その速度とその計測がここでは問題です。
図4は、まっすぐに張った平行フィーダ線の2本の線の中央の電界と磁界に、正弦波信号が伝播する様子です。
図4 電磁波を誘導するケーブル
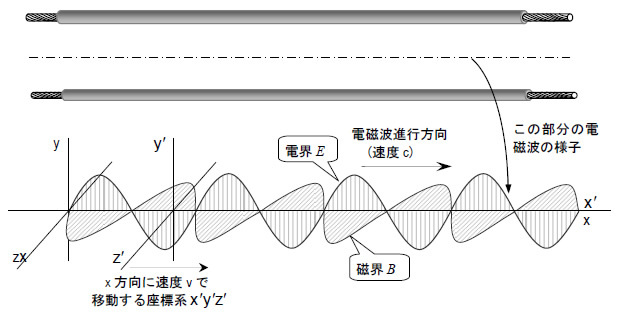
進行方向をx軸に合わせて、磁界Bと電界Eの関係を計算・考察するものです。磁界の向きと電界の向きは直交するので、ここでは電界の向きをz軸に合わせると、磁界の向きはy軸に合います。つまり電界Eはy成分だけをもち、磁界Bはz成分だけをもちます。
このときの時間と空間の関係は、次式になることが知られています。
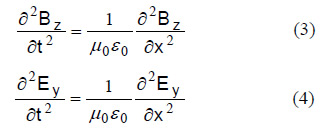
- μ0=真空の透磁率(1.2566×10-6 H/m )
- ε0=真空の誘電率(8.855×10-12 F/m)
伝播速度は =2.998×108 m/sです。同軸ケーブル構造でも、使用している絶縁体の誘電率と透磁率が真空のそれと同じであれば、伝播速度は同じです。
=2.998×108 m/sです。同軸ケーブル構造でも、使用している絶縁体の誘電率と透磁率が真空のそれと同じであれば、伝播速度は同じです。
波動の速度を簡単に計ってみる
この波動の速度は、フィーダ線に使っている絶縁体の誘電率によって若干異なりますが、真空の誘電率と同じならば、光の速度に等しいということも分かっています。
そこで、それをできるだけ簡単に計ってみようではありませんか?
大学のたいていの工学部や理学部なら備えている機器を使って、調べる方法の一つを提示しましょう。
必要なものは、信号発生器とオシロスコープ、10メートルほどの平行フィーダ線、あるい同軸ケーブル(図3)です。同軸ケーブルの方が、測定器や標準的な信号発信器との整合のためには都合がよいです。同軸ケーブルの特性インピーダンスは、50Ωあるいは75Ωに制作されているからです。
位相を使う実験のやり方
ケーブルは別段まっすぐに張らなくても、実験室の中にぐるりと1周させて、入り口と出口の電圧の波形をオシロスコープで計測するだけでよいのです(図5参照)。
図5 位相遅れの計測
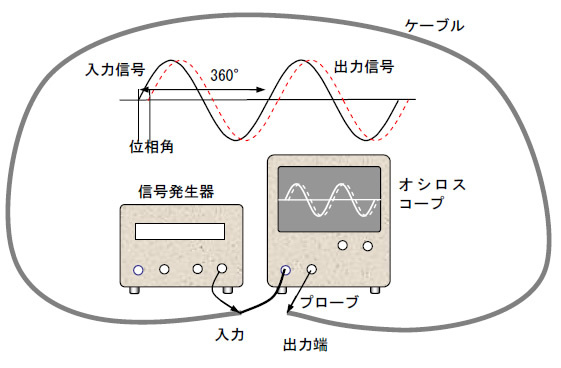
そして入り口の波形と出口の波形の時間遅れを見るのです。どんなタイプのオシロスコープでも可能な計測法が、連続した正弦波、あるいは三角波や方形波を入力端に加える方法です。
正弦波のときには、図5のような信号の遅れが観測されるはずです。このように電磁波の速度は、信号の位相というものによって観測できます。
信号の1サイクルの時間を360°として、出力が何度遅れているかというのが位相差です。この場合、周波数が高いほど位相差が顕著に見られるのですが、仮に3MHz(メガヘルツ)だとすると次のようになります。
3MHzの1サイクルは百万分の1秒であり、その時間の電磁波の進行距離は、3×108m/3×106=100mが波長です。
つまり100mのフィーダ線、あるいは同軸ケーブルならば、ちょうど1波長の遅れになるのです。ここでは10mですから、1/10サイクルの遅れであり、角度としては36°です。1MHzの信号でも、12°の遅れであり、オシロスコープで観測できるはずです。
繰り返しになりますが、この実験で気をつけることは、ケーブルの両端に特性インピーダンスに合わせた抵抗を接続することです。
信号発信器の内部で最初から接続されている終端抵抗の典型が50Ωです。信号発生器は、正弦波のほかに方形波も発生できます。その場合、終端抵抗が合っていないと波形が崩れるので、正しい実験をしているか、どこがおかしいのかの判断ができます。
実際には、ケーブルに資料する材料の誘電率のために、伝播速度が cからずれています。位相差の計測によって、そのずれがどれほどのものかが計算できることが分かっていだだけると思います。
写真は、いろいろなケーブルでこの実験をしているありのままの様子です。正確な計測実験ではないことご容赦ください。

電磁波を式で表す
これから問題とするのが、平行線を長くどこまでも張った場合のことです。弦の場合には、波動の速度が仮に秒速300mとすると、秒速100mの乗り物からからは200mの速度に見えるし、乗り物の速度が300/mであれば止まって見えるはずです。
アインシュタインの疑問は、光の場合でした。光も電磁波の一種です。彼の相対性理論では、平行フィーダ線にそってどんなに速い速度の航空機に乗って観測しても、観測者には電磁波の伝播速度が同じ速度cだということです。
電磁波の場合、電磁波の速度が観測者によって変わらないためには、電磁波の方程式がx' y' z' t'系でも、(3)式と同じ形で、次のようでなければなりません。
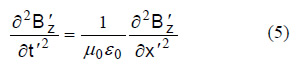
ただしダッシュ(’)はx' y' z' t'座標系で観測したときの電磁界を意味します。
教科書に書かれていないことが多い
初歩的な多くの電磁気学は、このことに触れていません。触れたとしても、マックスウェルの方程式から導かれる波動方程式は、自動的にそうなるのだと述べているものが多いです。
しかしそれをていねいに説明するためには、若干の疑問があります。2つの座標間での電磁界の関係をどのように与えているかが問題になるからです。
工学部のテキストでは、

とするのが一般的だと思います。
さらに、電界があってそこを導体が速度 vで通過したときには磁界が発生すると考えたのがマックスウェルです。
彼は式(4)に関連して、磁界を速度 vで通過すると電界が発生するとしました。これを2つの座標系の間の関係に変換して表現すると次の式です。

しかし、通常の速度では、右辺の第2項が無視できるので実質的に、

とすることが多いようです。
この問題点をしっかりと書いている教科書は違います。表1はその比較です。平行フィーダ線の中央の電磁波(BとE)の関係としてみてください。
電界と磁界の間には、時間と位置の関係とまったく同じローレンツ変換があるのです。これはアインシュタイン以降に、電磁気学の教科書を再構築していくプロセスで専門家たちによって整備された関係式だと思われます。
日本人による教科書として代表的なものは、大阪大学教授だった砂川重信氏の『理論電磁気学』(紀伊国屋書店)です。
表1 時空と電磁界のローレンツ変換(図3のxyz系とx'y'z'系の間の関係式)
| | 変数 | ローレンツ変換式 |
|---|
| 時空 | x:位置
t:時刻 | 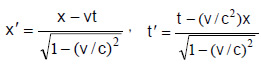 |
|---|
| 電磁現象 | E:電界強度
B:磁束密度 |  |
|---|
時空で不変なものインターバル
この時空で不変なものの代表は、確かに光速 cですが、より広く言うとインターバルであることを、『ピタゴラスの定理でわかる相対性理論』の6.12節や7.7節に書きました。
時空の不変量は、インターバルs2=(ct)2-(x2+y2+z2)です。
電磁界の不変量は、この形に類似して(cB)2-E2です。つまり、

が2つの座標間で成り立ちます。これは電磁界のインターバルのようなものです。ケータイで便利に使っている電磁波のインターバルともいえます。
このように波動には不思議な現象があります。筆者が大学で電子工学科の学生として取り組んだ卒業研究は、また不思議な波動でした。
それはガラス管の中に閉じ込めたアルゴンなどの稀ガスのプラズマに伝播する音波のような波動で、1方向にしか伝播しない移動縞というものです。
不思議というのは、発信源から波が遠ざかるのではなく、遠方から発信源に向かって進行してくる波動だからです。そんな波動がこの世にあるのかと読者は思われるに違いないないのですが、極めて不思議の国のことのようですが、本当にそうなのです。
次回はそれについて書いてみたいと思います。






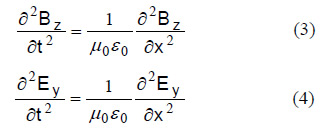
![]() =2.
=2.

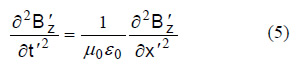
![]()
![]()
![]()
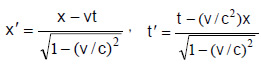

![]()


