今回は9.7節「開けてしまったパンドラの箱」（⁠212ページ）について書いてみました。有名なE＝mc²の法則です。

石油など温室効果ガスの利用を減らさないと地球環境が破壊されようとする今、原子力発電の意味を問い直されています。アインシュタインは原子力発電の基本の原理になる法則の発見に関する論文を1905年9月27に物理学年報に寄稿したのです。ただし、彼はこの論文で原子力発電という発想を述べているわけではありません。基本的に物体のエネルギーと質量あるいはより一般的に慣性の関係について、ある可能性を指摘しているように思われます。

この論文にまつわる盗作問題やハーゼンエールのことについては、すでに第2回に書いたのですが、今回は真正面から取り組みましょう。

原文を読むメリット

アインシュタインのことに興味を持つ人は大変に多いのですが、彼の論文を原文で読んだという人は少ないでしょう。大学の物理学科の学生でさえアインシュタインを原文で読む機会が与えられることもなく、自ら読もうという意欲を感じる暇がないかもしれません。

ここでは、特殊相対性原理に関する2番目の論文を読み下してみます。その原文は

• http://einstein-annalen.mpiwg-berlin.mpg.de/annalen/alphabetical

から入手できます。ここにはアルファベット順にタイトルが並んでいるので、Istで始まる論文をクリックします。

アインシュタインの文体は簡明で、ドイツ語特有の複雑な論理を展開してはいないと感じます。ドイツ語を第2外国語として勉強している大学生にはちょうどよい教材ではないかと思います。

筆者にとってもドイツ語は楽ではないことを白状します。40年以上も前に本当に仕方がなくてドイツ語でモータの設計に関する論文を書いたことはあるのですが、長いあいだ本気で読む必要性も少なくなったので、ほとんど忘れたようなものです。これを機会に文法と単語を思い出しながら読んで翻訳してみました。

若いときに、自分の考えたことを第2外国語で表現する試みから得たメリットもありました。2つ挙げます。

• (1)書く前に、読む必要がある。しかも自分の専門領域の論文を読むのがよい。筆者の場合は、モータの設計に関するドイツ語論文を数編精読し、その英訳をつくり、自分の英訳からドイツ語を復元する訓練をした。こうすることによって専門領域の動詞の使い方を習得できる。
• (2)相対性理論や量子力学は、ドイツ語を母語とする物理学者や数学者から生まれたが、これを読むときにドイツ文学や哲学など文系ドイツ語教師の指導では無理がある。通常の辞書を引きながらの解釈は、誤解と誤訳につながる。内容を完全に理解し批評できる指導者を得るのがベストだがそれは理想かもしれない。

こういうことを念頭において、本論文を日本語訳してみたのですが、ひょっとすると間違いもあるかもしれませんので、読者中に何か気がつく方がおられたらぜひご指摘をいただきたいと思います。

この論文の日本語訳はすでにあると思うのですが、筆者はあえてもっていません。原文を読んだあとで英語の定訳を見ているのですが、それはあくまで確認のためですし、若干の意訳があったりして疑問もあり、筆者にはわかりにくかったりする部分があります。

そこで、あくまでアインシュタインが綴った文章と数式をたどってみようと思います。

なお、英語版の論文　[Does the inertia of a body depend on its energy content?] は、

• http://www.fourmilab.ch/etexts/einstein/E_mc2/www/

から入手できます（アドレスは変更される可能性があります⁠）⁠。

モータ理論は時空の基本的な法則

この記事を書きながら筆者は、モータの理論(筆者のElektrodynamik)を作りなおそうとしています。ここで紹介するアインシュタインの論文でも一つの基礎としたマックスウェル方程式と、イギリスの物理学者Poyntingが提唱した電磁エネルギーの定理を基盤として、モータの原理は、時空の基本的な法則であるとする考え方です。それがまた地球温暖化を防ぐ手段にもなるのではあるまいかという発想です。

Poyntingの定理は1884年に発表された理論ですが、よく吟味するとそれはマックスウェルの方程式から誘導されるものです。筆者のモータ理論は、マックスウェル方程式とニュートン力学を基盤にしたものであるといえます。ちなみに、この論文の一年前のハーゼンエールの論文でE＝(3/4)mc²を導く中でも、Poyntingのエネルギー流が頻繁に引用されています。

さらにアインシュタインは、相対性原理を基盤として、空間の電磁エネルギーについてPoyntingの発想にはなかった思考を加えていますが、このことが重要だと思います。

こういうことに思いを馳せながら、電磁気学の議論の相手をしてくれる友人を喫茶店で待つ間の30分に今回の訳の草稿の7割ほど書くことができました。草稿は1時間ほどの仕事ですが、見直しと推敲はその数十倍の時間を要するものでした。

イラスト付き日本語訳

アインシュタインの論文が難しいと思うのは、図がないことです。そこで論文を理解するため下のようなイラストを作ってみました。

それでは、論文の日本語訳を以下に紹介します。

なお、現在では光速を小文字のcで表しますが、この当時のアインシュタインは大文字のVを使っていました。

物体の慣性はそのエネルギー量に関係するか？

本論文誌（Annalen der Physik、理学年報）に前回寄稿した電気力学の研究[1]の結果から、大変に面白いことが言えるのでここに以下記述する。

ここで私は、真空中のMaxwell-Hertzの方程式と空間の電磁エネルギー論をベースとして、さらに次の相対性原理を使う。

物理的システムの状態が従うところの法則は、2つの互いに平行に等速相対運動する座標を取ったとったとき、どちらにこの状態を委ねるべきかに関係ない（どちらでもよい）。

これらの基礎[2]に立脚して（さまざまの結果を得たのだが⁠）⁠、とりわけ凄いのが次の結果である。

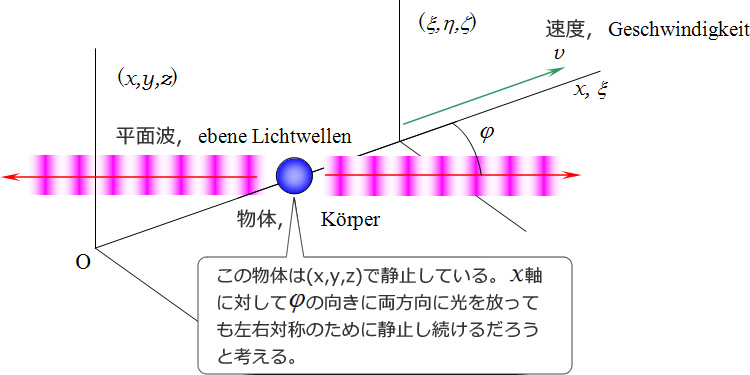
一つの光の平面波のシステムを(x, y, z)系で設定し、エネルギーlをもつものとする。光の放射の向きをx軸に対して角Φの方向にとる。もう一つの系(ξ, η, ζ)を設定して、この系の原点は (x, y, z)の原点に対してx軸の方向に一定の速度vで移動しているものとする。そのとき、系(ξ, η, ζ)におけるエネルギーl* は

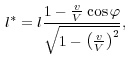
である(訳者注1)。ここでVは光速である。

この結果を使って次の論理を導こう。

系(x, y, z)に静止している物体をとりあげよう。そのエネルギーは系(x, y, z)に属するのだが、これをE₀とする。この系に対して速度vで相対的に運動している系(ξ, η, ζ)でのエネルギーをＨ₀とする。

この物体がx軸に対してΦの角度で（(x, y, z)で計測された(訳者注2)）L/2のエネルギーの平面波を放つものとする。また同時に反対方向にも同量を放つものとする。このとき物体は系(x, y, z)に静止している。

この事象においてエネルギーの法則が成立するはずであるし、しかも（相対性原理によって）2つの座標系に対して成立する。光の放射のあとのエネルギーをそれぞれの座標系に対してE₁およびＨ_１とすると、前述の関係を使うことによって次式が得られる。

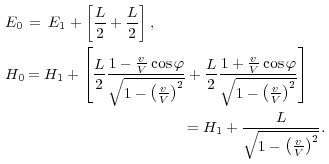
これらの式の差をとると、次式が得られる。

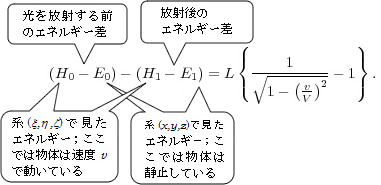
この式に現れるH－Eの2つの差形式は、単純な物理的な意味をもっている。HもEもこの同じ物体のそれぞれの系に属するエネルギーであるが、互いに相対的に運動しており、一方（系(x, y, z)）では物体が静止している。

よって次のことが明白である。

差 H－Eは、他方の系(ξ, η, ζ)における運動エネルギーKにCなる定数(単数)を加算しただけものである。ここでCとはエネルギーHおよびEに加算される任意の定数(複数)で決まる量である（訳者注3⁠）⁠。したがって次式が得られる。

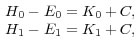
Cは光の放射中は変化しないので次式が得られる。

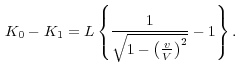
系(ξ, η, ζ)における物体の運動エネルギーは光の放射中によって減少するのだが、それは物体の性質に無関係な量である。運動エネルギーの差K₀－K₁は、電子の運動エネルギーのように速度に関係する。

v/Vの第４次以上の成分を無視すると次のように記すことができる。

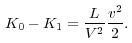
この式から直接次のことが言える。

ある物体がエネルギーLを光の放射の形で放出すると、その質量がL/V²だけ減る（訳者注5⁠）⁠。

ここでエネルギーが輻射（訳者注：光の放射）の形をとることが本質ではない（訳者注：どうでもよい）とすれば、次の一般的な推論に到達する。

物体の質量はそのエネルギー量（中身）の一つの尺度である。エネルギーがLエルグだけ変化（増減）すると、その質量はL/9×10²⁰グラムだけ変化（増減）することを意味する。

このエネルギー量がかなりの割合で変化する物体（例えばラジウム塩）を使って、本理論の証明がうまくできるかもしれない。もし、本理論が事実に対応すれば、放射は放出源の物体と吸収源の物体の間で慣性量（訳者注6）を輸送するといえる（1927年9月27日受付⁠）⁠。

脚注：

※1） A. Einstein: Ann. d. Phys.17. p.891. 1905.

※2） そこに使われている光速一定の原理がマックスウェル方程式にも自然に宿っている（訳者注4⁠）⁠。

訳者注：

1）1905年6月論文で、電磁波のエネルギー密度と空間の大きさを2つの系で見比べることによって、この変換式を導いている。

2）原文にはL/2（relativ zu (x、y、z) gemessen）とあり、英語版ではenergy 1/2L measured relatively to (x, y, z)となっているので、直訳ふうに「(x, y, z)に対して相対的に計測されたエネルギー1/2L」としたくなるが、アインシュタインは(ξ, η, ζ)系では異なる計測値になることを念頭においていたと考えて、筆者の訳としては、単に「⁠（⁠(x, y, z)で計測された）L/2のエネルギー」とした。

3）ここが難解。アインシュタインは運動エネルギーについて思考するにあたって、運動量の積分などさまざまのことを考えたと思われる。積分に関連して積分定数にも考えが及んだのだろう。たとえば Hに対して積分定数のようなAが加算され、EにはBが加算されるものとすればH－EではC＝A－Bということになる。原文にある単数と複数の微妙な綾が翻訳で落ちると意味を推測することができない。

特殊相対性理論をしっかりと解説している参考書として筆者があげると、平凡社の1973年版世界大百科事典の「そうたいせいりろん」であり、著者は、当時京都大学教授の林忠四郎氏である。そこにはこのあたりに関係すると思われる積分定数について書いている部分があり、そこを引用してみよう。

････単位時間にする仕事の量、すなわち工率は先の運動方程式を用いて計算すると、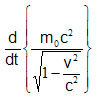

となる。この工率はまた質点のエネルギーEの増す割合に等しいから、積分して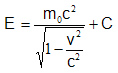

が得られる。エネルギーを仕事の蓄積と考えるかぎりは上の定数はどうとってもさしつかえない。たとえば速さが0のときにエネルギーも0と定めると定数として－mc²をとればよく、このとき十分小さい速さに対して分母を展開すると上式のEはニュートン力学の運動エネルギーm₀v²/2に一致する。しかしながらC＝0に選んで、速さが0の質点もいわゆる静止エネルギーm₀c²をもつものと考えると運動量とエネルギーを統一的に扱うことができる。

ここで興味深いのが、アインシュタインはこの段階で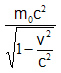

の形を出していないことである。ここには深い思慮があったに違いないと思われる。

もうひとつ参考になる本として、アインシュタイン自身が書いてイギリスのシェフィルド大学のRobert Lawsonが翻訳した A.Einstein：Relativity、 Crown Publisher － The special and general theory、 New York がある。この論文に関するテーマを扱っている部分を見ると、英語に訳された言葉はやさしいのだがほしい説明がないために理解は困難。アインシュタインの頭脳にとっては当たり前のことが私どもには当たり前ではないように思われる。

4）Das dort benutzte Prinzip der Konstanz der Lichtgeschwindigkeit ist naturlich in den Maxwellschen Gleichungen enthalten. ここでnaturlichが、もちろんとか当然という意味なのか、あるいは自然になのか訳者には不明。6月論文でアインシュタインはこれを説明しているが、本書執筆中、著者2人はこれを別のすっきりとした論理で確かめるための計算をした。そのときに整理したのが参考資料1である。専門用語を使うとローレンツ共変形になっていると言う。（⁠英訳ではof courseと訳されているが、訳者は自然にの意味に近いnaturallyと解釈したい⁠）⁠。

5）(ξ, η, ζ)系では、物体が速度vで動いているので質量をmとすれは、運動エネルギーKは1/2mv²である。光の放射の前後に運動エネルギーの差があるとすれば、それは質量の差Δmが発生したと考える。つまりK₀－K₁＝1/2Δmv²として、これが(L/V²)(v²/2)に等しいとすると1/2(L/V²)V²＝1/2Δmv²であり、両辺から1/2V²を取り去るとΔm＝L/V²となる。

最近では一般的にエネルギーとしてLに代わってEを用い、Vに代わってcとする。また質量の差を単にmとするとE＝mc²と記される。

6）Tragheitは英語のinertiaで慣性であるが、より具体的な量を意味するものと解釈して、慣性量とした。

読後感

「ピタゴラスの定理でわかる相対性理論」でも書いたのですが、アインシュタインはユークリッド幾何の論理展開に感銘していました。現在でも、多くの中学生や高校生の中に同じような感銘を受ける少年はいると思うのですが、アインシュタインの理解力というか吸収力は並外れたレベルではなかったかと思われます。それはユークリッドレベルだったかとさえ感じます。ユークリッド幾何は「当たり前」の公理から、当たり前とは思えない定理を導いていく凄さを教室で感じさせることができます。

マイケルソン-モーレイの実験から、アインシュタインが時間や距離に関して当たり前ではない結論を導いて6月論文を書き、その後も思考と計算に没頭してさまざまな理論的帰結を得ながら、当たり前ではない公理から驚くべき物理の法則を導いたのです。

この論文はきわめて短く、序論のようなものはほとんどありません。単刀直入です。しかし難解なのが定数Cに関係する論理です。本来なら丁寧に書きたいあるいは書くべきものがあったと思うのですが、省いています。その部分について彼の思考をどのように推察してよいのかわかりません。ここが詳しく記されていないのが残念というより悔しい思いがします。しかし幸い宇宙物理学者の林先生がなるほどいう解釈をなさっていました。

アインシュタインのこの論文の最後の1文は意味深長だと思います。

余談「質量とMasse」

Die Masse eines Körpers is ein Maß für dessen Energieinhalt. （⁠ある物体の質量は、その物体のエネルギー量の一つの尺度である。）

ßはスイスのドイツではssになります。ガウスとボヤイの文通の資料（ガウス書簡集：「ピタゴラスの定理でわかる相対性理論」の参考資料22）でもそうなっているので、MasseとMassの区別がうっかり判然としません。

Masseは女性名詞で質量（英語のmass）でありMaßは中性名詞で度量とか軽量で英語ではmeasureです。Einは英語のaにあたるのですが、日本語として一つのと強調すべきかどうか迷います。

これら２つの単語が語源を共通にするのかどうか、筆者にはわかりません。 ちなみに中国語の質量は、物理学では日本語と同じ意味ですが、通常は品質の意味に使われます。