人に話したくなる数学おもしろ定理
定理は、遠い世界のことと思われがちです。でも定理の歴史をみてみると、もっと生活に密着した存在だったのです。例えば、古代文明時代は、国を治めるために、自然や暦を知って政を行う必要がありました。そのために当時の数学者達は、天文学に精通していました。
また統治者が権力を示すための大規模な土木建築の必要から、測量に秀でた数学者が活躍しました。
つまり、定理はその時代の社会の必要性に応えるために生まれてきたのです。
その一例としてここで問題。次のような直線a、b、cで囲まれた形の土地の面積を求めてみましょう。
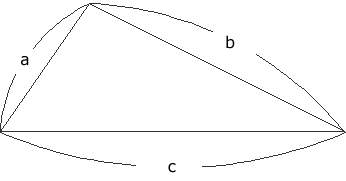
これは、面積=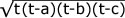 というヘロンの公式を用いて求められます。三角形の面積は高さがわからない場合はそう簡単には求められません。ここでt=(a+b+c)/2 ……(周囲の長さの半分)。でも、今から約2000年前のアレクサンドリアの数学者であるヘロンは、周囲の長さを測れば面積が求められることを示しました。とても実用的ですね。
というヘロンの公式を用いて求められます。三角形の面積は高さがわからない場合はそう簡単には求められません。ここでt=(a+b+c)/2 ……(周囲の長さの半分)。でも、今から約2000年前のアレクサンドリアの数学者であるヘロンは、周囲の長さを測れば面積が求められることを示しました。とても実用的ですね。
このような定理に関する面白い話が満載されているのが『人に話したくなる数学おもしろ定理』です。
「ピタゴラスの定理でわかる相対性理論」
誰もが知っているピタゴラスの定理は、a2+b2=c2で表されます。これを掘り下げていくと、どうなるでしょうか。
例えば球面上の直角三角形の辺に関するピタゴラスの法則は、cos(a)=cos(b)・cos(c)ですが、ちょっと模索していくと、a2+b2=c2という形が見えてきます。
では、双曲幾何でのピタゴラスの定理はどうなるでしょうか。cosh(a)=cosh(b)・cosh(c)という定理が成り立つのです。どうやらつながりがありそうですね。このつながりをたどっていくと、なんとアインシュタインの相対性理論にまで行き着いてしまうのです。
本書では幾何学にはじまり、球面幾何をたどって、双曲幾何、そして相対性理論までの数学の歴史を紐解きながら、その時代で活躍した偉大な数学者たちのユニークなエピソードを交えて、数学のエッセンスを一つのストーリーとしてまとめたものです。ピタゴラスの定理をご存知であれば、わくわくしながら読むことができます。
化学の不思議
私たちの周囲には、見過ごしがちな面白い現象が起こっています。例えばオンザロックや冷水を飲んでいると、コップがいつの間にか汗をかいています。拭き取ってもしばらくするとまた汗をかきます。
また、紙に火をつけると一気に燃えますが、ロウソクに火をつけても一気に燃えません。不思議ですね。
このように、ちょっと見る目を変えることで、身近で起こっていることが、実は化学の話になってくるのです。
本書では、身近なテーマを選び、化学の知識が身につくように、とてもわかりやすく解説しています。

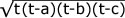 というヘロンの公式を用いて求められます。三角形の面積は高さがわからない場合はそう簡単には求められません。ここでt=(a+b+c)/2 ……
というヘロンの公式を用いて求められます。三角形の面積は高さがわからない場合はそう簡単には求められません。ここでt=(a+b+c)/2 ……