式の左辺と右辺の値が一致しないのに、なぜ正しいんだ？　いかにも無限になりそうなのに、なぜか無限にならない？　紐を巻いたような式や、絵記号を使ったこの式は何なんだ？　世の中は、実におかしな数式があふれている。そんな視線で物理や数学の「名式」を眺めてみると、別の光景が広がってくる。アインシュタインが発表した世界でいちばん有名な数式“⁠E＝mc²⁠”だって、今まで見えなかった裏側まで見えてくるというものだ。このコラムでは一つ“⁠へんな数式⁠”を選んでみよう。

生き物の公式

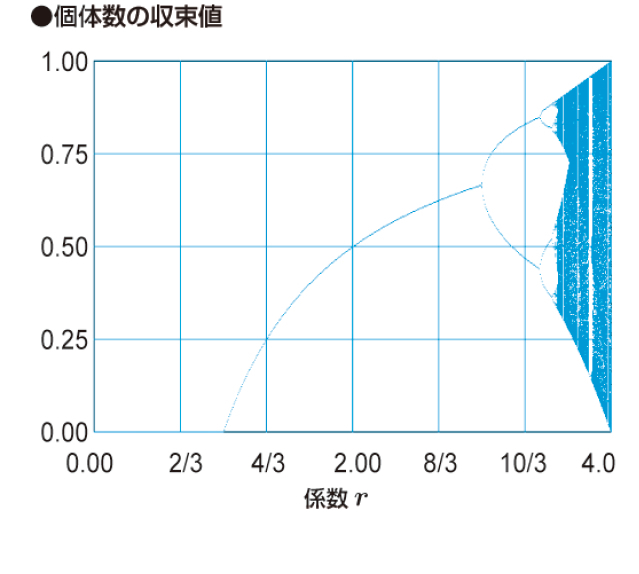
野原のカエルやネズミは増えたり減ったりするが、これを予測する式があるという。アメリカの数理生物学者ロバート・メイが発表した「ロジスティック写像」と呼ばれるものだ。それは

• X_n+1＝rX_n（1－X_n）

の形をしている。X_nというのは、ある時刻（ある年）におけるカエルの密度、X_n+1というのは、次の時刻（翌年）における密度を表す。これが意味するところはこうだ。ある時刻の密度は“⁠前の時刻の密度⁠”に比例するが、それとともに“⁠1－前の時刻の密度⁠”⁠、つまり増えることができる余力にも比例する。

式のなかに係数rが何気に使われているが、これがカエルの将来を大きく左右するクセ者なのだ。

係数rが1以下だと、カエルは絶滅に向けて減少していく。そして係数rが1より大きく3以下だと、一定の密度に向かって進む（グラフ1⁠）⁠。

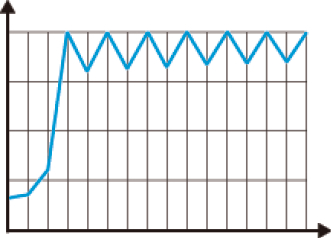
次は係数rが3より大きく3.57以下だと、2つの値を行ったり来たりするようになる（グラフ2⁠）⁠。

劇的に変化するのは次である。つまり係数rが3.57より大きいと、めちゃくちゃな増減を示して、どの値にも向かわなくなるのだ（グラフ3⁠）⁠。

ある生物が異常繁殖したり激減したりする理由はさまざまだろうが、背後にはこのような簡単な数式が潜んでいるかもしれない。細菌の流行や人口の増加など、一見すると指数関数的に増加するように比喩されるものでも、食物や空間には上限があるのだから、このロジスティック写像の考えが当てはまる。そしてこの式は自然界が示す「複雑性」を表している式でもあるのだ（グラフ4⁠）⁠。