今回からのお題は、
3次元空間の真ん中に箱を置いて回す
まずは、
new PrimitiveCubePrefab(幅, 高さ, 奥行き, 水平分割数, 垂直分割数, 奥行き分割数, 6面テクスチャ)だが、

前述のとおり、
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
function initialize() {
cube = createCube(400, 400, 400, directionalLight);
}
function createCube(width, height, depth, light) {
var material = new TriangleMethodMaterial();
var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
.getNewObject();
cube.material = material;
material.lightPicker = new StaticLightPicker([light]);
return cube;
}これで3次元空間の真ん中にテクスチャの貼られた立方体が置かれ、

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var DirectionalLight = require("awayjs-display/lib/entities/DirectionalLight");
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var TriangleMethodMaterial = require("awayjs-methodmaterials/lib/TriangleMethodMaterial");
var view;
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
var timer;
function initialize() {
var directionalLight = createDirectionalLight(0.5, 0xFFFFFF);
view = createView(240, 180, 0x0);
cube = createCube(400, 400, 400, directionalLight);
view.scene.addChild(cube);
AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
AssetLibrary.load(new URLRequest(imageDiffuse));
timer = new RequestAnimationFrame(rotate);
timer.start();
view.render();
}
function createView(width, height, backgroundColor) {
var defaultRenderer = new DefaultRenderer();
var view = new View(defaultRenderer);
view.width = width;
view.height = height;
view.backgroundColor = backgroundColor;
return view;
}
function createCube(width, height, depth, light) {
var material = new TriangleMethodMaterial();
var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
.getNewObject();
cube.material = material;
material.lightPicker = new StaticLightPicker([light]);
return cube;
}
function createDirectionalLight(ambient, color) {
var light = new DirectionalLight();
light.ambient = ambient;
light.color = color;
return light;
}
function onResourceComplete(eventObject) {
var assets = eventObject.assets;
var material = cube.material;
material.texture = assets[0];
view.render();
}
function rotate(timeStamp) {
cube.rotationX = (cube.rotationX + 1) % 360;
cube.rotationY = (cube.rotationY + 1) % 360;
view.render();
}立方体を中心に三角関数でカメラを回す
つぎは、
カメラの向きは後に回し、
x = 距離×cos角度
y = 距離×sin角度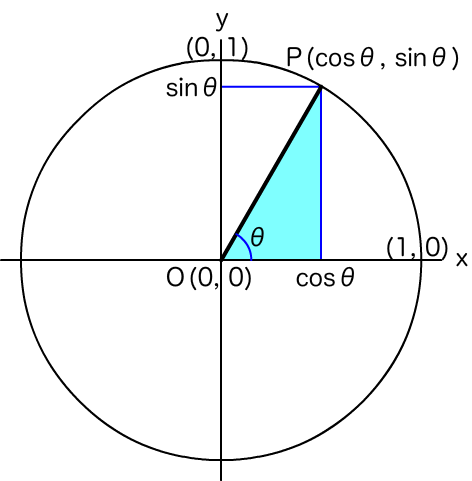
では、
カメラを動かす関数
setCamera(カメラ, 距離, 角度)前掲コード1は、
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var ORIGIN = new Vector3D();
var angle = -Math.PI / 2;
var distance = 1500;
function initialize() {
setCamera(view.camera, distance, angle);
}
function rotate(timeStamp) {
// cube.rotationX = (cube.rotationX + 1) % 360;
// cube.rotationY = (cube.rotationY + 1) % 360;
var camera = view.camera;
angle += timeStamp / 2000;
setCamera(camera, distance, angle);
}
function setCamera(camera, distance, angle) {
camera.x = Math.cos(angle) * distance;
camera.z = Math.sin(angle) * distance;
camera.lookAt(ORIGIN);
}この機会に、
var stageWidth = 240;
var stageHeight = 180;
function initialize() {
// view = createView(240, 180, 0x0);
view = createView(stageWidth, stageHeight, 0x0);
}これで、

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var DirectionalLight = require("awayjs-display/lib/entities/DirectionalLight");
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var TriangleMethodMaterial = require("awayjs-methodmaterials/lib/TriangleMethodMaterial");
var view;
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
var timer;
var ORIGIN = new Vector3D();
var angle = -Math.PI / 2;
var distance = 1500;
var stageWidth = 240;
var stageHeight = 180;
function initialize() {
var directionalLight = createDirectionalLight(0.5, 0xFFFFFF);
view = createView(stageWidth, stageHeight, 0x0);
cube = createCube(400, 400, 400, directionalLight);
setCamera(view.camera, distance, angle);
view.scene.addChild(cube);
AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
AssetLibrary.load(new URLRequest(imageDiffuse));
timer = new RequestAnimationFrame(rotate);
timer.start();
view.render();
}
function createView(width, height, backgroundColor) {
var defaultRenderer = new DefaultRenderer();
var view = new View(defaultRenderer);
view.width = width;
view.height = height;
view.backgroundColor = backgroundColor;
return view;
}
function createCube(width, height, depth, light) {
var material = new TriangleMethodMaterial();
var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
.getNewObject();
cube.material = material;
material.lightPicker = new StaticLightPicker([light]);
return cube;
}
function createDirectionalLight(ambient, color) {
var light = new DirectionalLight();
light.ambient = ambient;
light.color = color;
return light;
}
function onResourceComplete(eventObject) {
var assets = eventObject.assets;
var material = cube.material;
material.texture = assets[0];
view.render();
}
function rotate(timeStamp) {
var camera = view.camera;
angle += timeStamp / 2000;
setCamera(camera, distance, angle);
view.render();
}
function setCamera(camera, distance, angle) {
camera.x = Math.cos(angle) * distance;
camera.z = Math.sin(angle) * distance;
camera.lookAt(ORIGIN);
}すでに述べたとおり、
x = 距離×cos角度×比率
y = 距離×sin角度試しに、
function setCamera(camera, distance, angle) {
camera.x = Math.cos(angle) * distance * 0.5;
camera.z = Math.sin(angle) * distance;
camera.lookAt(ORIGIN);
}

原点からの円周上に複数のオブジェクトを並べる
真ん中に置いた箱の周りに、
cloneMesh(複製もとオブジェクト, 数)複製のオブジェクトをつくったら、
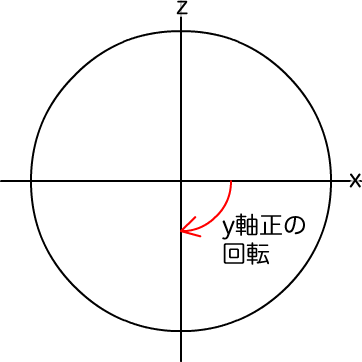
getPolarPosition(距離, 角度)オブジェクトの位置は、
オブジェクトを複製する関数
function initialize() {
cloneMesh(cube, 5);
}
function cloneMesh(mesh, count) {
var scene = view.scene;
var distance = 1000;
var degrees = 360 / count;
for (var i = 0; i clone();
var rotationY = degrees * i;
var position = getPolarPosition(distance, rotationY);
clone.x = position.x;
clone.y = position.y;
clone.z = position.z;
clone.rotationY = rotationY;
scene.addChild(clone);
}
}
function getPolarPosition(distance, rotationY) {
var vector = new Vector3D();
vector.x = distance * Math.cos(-rotationY * Math.PI / 180);
vector.z = distance * Math.sin(-rotationY * Math.PI / 180);
return vector;
}ひとつ補っておきたいのは、
これで、

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var DirectionalLight = require("awayjs-display/lib/entities/DirectionalLight");
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitiveCubePrefab = require("awayjs-display/lib/prefabs/PrimitiveCubePrefab");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var TriangleMethodMaterial = require("awayjs-methodmaterials/lib/TriangleMethodMaterial");
var view;
var cube;
var imageDiffuse = "assets/trinket_diffuse.jpg";
var timer;
var ORIGIN = new Vector3D();
var angle = -Math.PI / 2;
var distance = 1500;
var stageWidth = 240;
var stageHeight = 180;
function initialize() {
var directionalLight = createDirectionalLight(0.5, 0xFFFFFF);
view = createView(stageWidth, stageHeight, 0x0);
cube = createCube(400, 400, 400, directionalLight);
setCamera(view.camera, distance, angle);
view.scene.addChild(cube);
cloneMesh(cube, 5);
AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
AssetLibrary.load(new URLRequest(imageDiffuse));
timer = new RequestAnimationFrame(rotate);
timer.start();
view.render();
}
function createView(width, height, backgroundColor) {
var defaultRenderer = new DefaultRenderer();
var view = new View(defaultRenderer);
view.width = width;
view.height = height;
view.backgroundColor = backgroundColor;
return view;
}
function createCube(width, height, depth, light) {
var material = new TriangleMethodMaterial();
var cube = new PrimitiveCubePrefab(width, height, depth, 1, 1, 1, false)
.getNewObject();
cube.material = material;
material.lightPicker = new StaticLightPicker([light]);
return cube;
}
function cloneMesh(mesh, count) {
var scene = view.scene;
var distance = 1000;
var degrees = 360 / count;
for (var i = 0; i < count; i++) {
var clone = mesh.clone();
var rotationY = degrees * i;
var position = getPolarPosition(distance, rotationY);
clone.x = position.x;
clone.y = position.y;
clone.z = position.z;
clone.rotationY = rotationY;
scene.addChild(clone);
}
}
function createDirectionalLight(ambient, color) {
var light = new DirectionalLight();
light.ambient = ambient;
light.color = color;
return light;
}
function onResourceComplete(eventObject) {
var assets = eventObject.assets;
var material = cube.material;
material.texture = assets[0];
view.render();
}
function rotate(timeStamp) {
var camera = view.camera;
angle += timeStamp / 2000;
setCamera(camera, distance, angle);
view.render();
}
function setCamera(camera, distance, angle) {
camera.x = Math.cos(angle) * distance;
camera.z = Math.sin(angle) * distance;
camera.lookAt(ORIGIN);
}
function getPolarPosition(distance, rotationY) {
var vector = new Vector3D();
vector.x = distance * Math.cos(-rotationY * Math.PI / 180);
vector.z = distance * Math.sin(-rotationY * Math.PI / 180);
return vector;
}


