第42回　Vector3Dクラスの3次元空間座標とインスタンスへの描画

今回からまた3次元空間の話に戻る。新たに学ぶクラスはVector3Dだ。名前が示すとおり、3次元空間座標（位置ベクトル）を扱う。初めのお題は例によって、四角形を3次元空間で水平に回してみる。第35回「Matrix3Dクラスによる座標変換」のスクリプト1と同じく、マウスポインタの水平位置に応じてアニメーションさせたい（第35回図3再掲⁠）⁠。

Vector3DインスタンスをMatrix3Dオブジェクトで座標変換する

まず、Vector3Dオブジェクトは、xyzの3次元座標をそれぞれVector3D.x/Vector3D.y/Vector3D.zプロパティとしてもつ。2次元平面の座標については、第22回「MovieClipシンボルにクラスを定義する」でPointクラスを学んだ。Vector3Dクラスは、その3次元版といえる。コンストラクタメソッドVector3D()でインスタンスをつくるとき、xyz座標値は引数として渡せばよい[1]⁠。引数がなければ、初期値0として扱われる。

new Vector3D(x座標, y座標, z座標)

Vector3Dインスタンスも、Matrix3Dクラスを使って座標変換できる。メソッドは、Matrix3D.transformVector()だ。引数にVector3Dインスタンスを渡すと、変換の加えられた新たなVector3Dオブジェクトが返される。

Matrix3Dオブジェクト.transformVector(Vector3Dオブジェクト)

たとえば、3次元空間座標(100, 0, 0)をy軸で90度回してみよう。新しい（デフォルトの）Matrix3Dオブジェクトに加える回転なので、Matrix3D.prependRotation()メソッドで足りるだろう。

var myVector3D:Vector3D = new Vector3D(100, 0, 0);
var myMatrix3D:Matrix3D = new Matrix3D();
myMatrix3D.prependRotation(90, Vector3D.Y_AXIS);
trace(myMatrix3D.transformVector(myVector3D));

変換されたVector3Dインスタンスの座標情報が、以下のように[出力]される（図1⁠）⁠。x軸上の座標(100, 0, 0)をy軸正方向に対して90度時計回りに変換すれば、z軸上負の方向つまり手前に移る。その座標は(0, 0, -100)となる。

Vector3D(6.12323420998628e-15, 0, -100)

なお、[出力]されたVector3Dインスタンスのx座標が「6.123…e-15」というのは、小数点以下0が14桁続く極めて小さな数値で、誤差を含んだ0と考えればよい[2]⁠。

さて、これで3次元座標が自由に変換できる。しかし、まだ大事なことが残っている。Vector3Dオブジェクトの座標を回しても、そのままでは見えない。xyz座標の値を[出力]しただけでは、回っているのかどうかがわからないだろう。

1.23e-4 = 1.23×10^-4 = 0.000123

Spriteインスタンスに直線を描く

3次元空間座標を行列変換しただけでは、座標値は求められても、その振る舞いが目に見えない。座標に対して線を描いたり、塗ったりする作業が必要になる。そこで、複数の座標の間を線（ワイヤーフレーム）で結ぶことにする。使うのは第33回「遠近法の投影」でもご紹介したGraphicsクラスのメソッドだ。描画用のSpriteインスタンスをつくり、そのSprite.graphicsプロパティのGraphicsオブジェクトにベクターの線を描く。

直線の描き方は、[線ツール]と同じ要領だ（図2⁠）⁠。線の太さやカラーといったスタイルを決めてから、始まりと終わりの位置を定める。線のスタイルを決めるメソッドはGraphics.lineStyle()、始まりと終わりはGraphics.moveTo()およびGraphics.lineTo()で指定する。

Graphicsオブジェクト.lineStyle(太さ、カラー, アルファ)
Graphicsオブジェクト.moveTo(x座標, y座標)
Graphicsオブジェクト.lineTo(x座標, y座標)

ステージ中央に置いたSpriteインスタンスに、100ピクセル四方の正方形を描いてみよう。線の太さは2ポイント、カラーは青（0x0000FF）とする。Spriteインスタンスの基準点に対して、水平・垂直とも±50ピクセルの大きさで4辺を描けばよい。なお、Graphics.lineTo()メソッドを呼出すと、その引数の座標がつぎの描き始めの位置になる。したがって、連続した直線を描くなら、Graphics.moveTo()メソッドは初めに呼出すだけでよい。

var mySprite:Sprite = new Sprite();
// インスタンスから取出したGraphicsオブジェクトを変数に代入
var myGraphics:Graphics = mySprite.graphics;
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
addChild(mySprite);
// Graphicsクラスのメソッドで線描
myGraphics.lineStyle(2, 0x0000FF);
myGraphics.moveTo(-50, -50);
myGraphics.lineTo(50, -50);
myGraphics.lineTo(50, 50);
myGraphics.lineTo(-50, 50);
myGraphics.lineTo(-50, -50);

この座標を線で描く処理は、後々使いやすいような仕組みに整えておこう。空間を座標で扱い出すと、座標の数はあっという間に増えてしまう。数に惑わされないよう、ふたつ手を加える。第1に、座標はまとめておく。xy座標はPointオブジェクトとし、さらにそれら座標群を配列に納める。第2に、描画は関数として定義する。引数には、Pointがエレメントに納められた配列を渡す。

でき上がったフレームアクションが、以下のスクリプト1だ。配列（変数vertices）に4つのPointインスタンスを納めた。描画する関数（xDrawLines()）は、配列からPointインスタンスを取出し、Graphicsクラスのメソッドにより順に直線を描いている。処理の結果は、前のフレームアクションと変わらない（前掲図3参照⁠）⁠。

スクリプト1　配列から取出したPointインスタンスの座標にしたがってSpriteに線を描く

// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var vertices:Array = new Array();   // 座標のPointインスタンスを納める配列生成
var myGraphics:Graphics = mySprite.graphics;
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
// xy座標をPointインスタンスにして配列に納める
vertices.push(new Point(-nUnit, -nUnit));
vertices.push(new Point(nUnit, -nUnit));
vertices.push(new Point(nUnit, nUnit));
vertices.push(new Point(-nUnit, nUnit));
addChild(mySprite);
xDrawLines(vertices);
// 配列からPointインスタンスを取出して線描する関数
function xDrawLines(vertices:Array):void {
  var nLength:uint = vertices.length;
  var myPoint:Point = vertices[nLength - 1];
  myGraphics.lineStyle(2, 0x0000FF);
  myGraphics.moveTo(myPoint.x, myPoint.y);
  for (var i:uint = 0; i < nLength; i++) {
    myPoint = vertices[i];
    myGraphics.lineTo(myPoint.x, myPoint.y);
  }
}

Vectorクラスと3次元空間から2次元平面への変換

いよいよスクリプトに3次元座標の扱いを組込もう。また、ふたつ手を加える。第1に、座標を入れるオブジェクトは、配列からVectorインスタンスに変える。このクラスはVector3Dとは違い、座標には関係ないので注意してほしい。VectorはいわばArrayを最適化したクラスだ。第2に、3次元空間の座標をスクリーンに描画するためには、2次元平面の座標に変換しなければならない。そのための関数を定義する。

まず、Vectorクラスは、Flash Player 10から備わった。Arrayクラスと異なり、エレメントは型指定され、その処理が速い。しかし、値にインデックスをつけてインスタンスに納めるという役割は配列と同じだ[3]⁠。Vectorクラスを使うための条件は、おもにつぎのふたつだ。

Vectorクラスを使うための条件：

エレメントにひとつのデータ型を定める
インデックスが連番になる

第1に、Vectorインスタンスをつくるときには、必ずエレメントの型（ベース型）が定められていなければならない。第2に、エレメントのインデックスは連番でなければならず、インスタンスの長さ（Vector.lengthプロパティ）より大きなインデックスには値が入れられない。これらの条件を満たすFlash Player 10以降のコンテンツなら、ArrayよりVectorクラスを使うことがお勧めだ。

Vectorクラスでひとつとても変わっているのは、インスタンスをつくるコンストラクタメソッドの呼出しだ。エレメントのベース型をコンストラクタの後に続くドット（.）と山括弧（<>）の中に書く。そして、変数や引数のデータ型も同じように定める。

var 変数:Vector.<ベース型> = new Vector.<ベース型>()

備わっているプロパティやメソッドは、Arrayクラスと多くが同じだ。エレメント数つまりオブジェクトの長さはVector.lengthプロパティで扱い、エレメントはVector.push()メソッドで加える。たとえば、ベース型がVector3DのVectorインスタンスをつくり、Vector3Dオブジェクトのエレメントを納めたうえですべて取出す処理はつぎのようになる（図4⁠）⁠。

var nUnit:Number = 50;
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
var nLength:uint = vertices.length;
for (var i:uint = 0; i < nLength; i++) {
  var myVector3D:Vector3D = vertices[i];
  trace(myVector3D);
}

つぎに、3次元空間の座標を、2次元平面に変換する関数の定義だ。ActionScript 3.0には、3次元座標空間に直接描画するクラスはない。オブジェクトが遠くにいくほど小さくなったり、同じ座標の間が狭まって見えるのは、2次元平面の画面に映し出したときの話だ。3次元空間の座標が伸縮する訳ではない。この2次元平面への投影は、別に計算しなければならない。

そこで定義する関数は、3次元空間座標から単純にxyの座標値を取出す。すでに予想した読者もあるだろうが、これは仮組みだ。正しい投影は次回に解説する。ただ、変換の関数を予め組入れておくことによって、投影以外の動きを完成させよう。以下がその関数定義（xGetVertices2D()）だ。Vector3Dオブジェクトが納められたVectorインスタンスを引数として受取り、PointオブジェクトのVectorインスタンスを返す。

function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  var vertices2D:Vector.<Point> = new Vector.<Point>();
  var nLength:uint = myVertices.length;
  for (var i:uint = 0; i < nLength; i++) {
    var myVector3D:Vector3D = myVertices[i];
    vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  }
  return vertices2D;
}

たとえば、前掲スクリプトでつくったVector3Dベース型のVectorインスタンスをこの関数（xGetVertices2D()）に渡せば、xy座標がPointオブジェクトのエレメントに納められたVectorインスタンスが返される（図5⁠）⁠。

前掲スクリプト1と組合わせて、3次元空間の座標から2次元平面のワイヤーフレームを描いてみよう。3次元座標は四角形の4頂点とし、1辺の半分の長さを変数（nUnit）で与える。各座標の初期値は下図6のように、z座標値を0としておく。なお、各頂点につけた0から始まる整数は、Vectorオブジェクトに納めるインデックスだ。

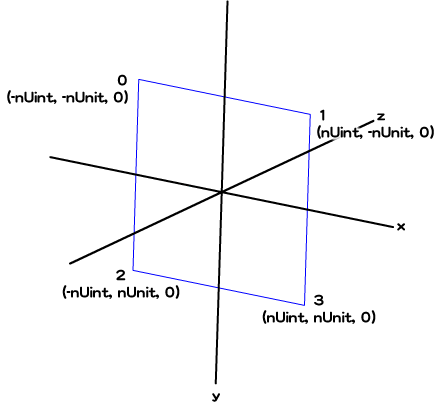
フレームアクションは、つぎのスクリプト2のようになった。描かれる正方形は、前掲図3と変わらない。なお、線を描く関数（xDrawLines()）は、スクリプト1とは少し変えて、引数はArrayでなくVectorオブジェクトで受け取ることにした。

スクリプト2　3次元空間の頂点座標から2次元平面のワイヤーフレームを描く

// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
var myGraphics:Graphics = mySprite.graphics;
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
addChild(mySprite);
var vertices2D:Vector.<Point > = xGetVertices2D(vertices);
xDrawLines(vertices2D);
function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  var vertices2D:Vector.<Point> = new Vector.<Point>();
  var nLength:uint = myVertices.length;
  for (var i:uint = 0; i < nLength; i++) {
    var myVector3D:Vector3D = myVertices[i];
    vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  }
  return vertices2D;
}
function xDrawLines(vertices2D:Vector.<Point>):void {
  var nLength:uint = vertices2D.length;
  var myPoint:Point = vertices2D[nLength - 1];
  myGraphics.clear();
  myGraphics.lineStyle(2, 0x0000FF);
  myGraphics.moveTo(myPoint.x, myPoint.y);
  for (var i:uint = 0; i < nLength; i++) {
    myPoint = vertices2D[i];
    myGraphics.lineTo(myPoint.x, myPoint.y);
  }
}

マウスポインタの水平位置に応じて3次元座標を水平に回転する

これでようやく前述「Vector3DインスタンスをMatrix3Dオブジェクトで座標変換する」で紹介した3次元空間座標の回転が加えられ、画面で描画を確かめられる。3次元座標を回す処理は関数（xTransform()）として定めよう。引数にはVector3Dベース型のVectorオブジェクトとy軸回りの回転角を渡す。

function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
  var nLength:uint = myVertices.length;
  var myMatrix3D:Matrix3D = new Matrix3D();
  myMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
  for (var i:int = 0; i<nLength; i++) {
    myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  }
}

前掲スクリプト2にこの関数を組込んだうえで、アニメーション（DisplayObject.enterFrameイベント）のリスナー関数（xRotate()）を加える。リスナー関数はマウスポインタの水平位置から回転角を定め、3次元座標を回すという仕組みだ（スクリプト3⁠）⁠。今回のスクリプティングはここまでにする。

スクリプト3　3次元空間の頂点座標にもとづいて2次元平面にワイヤーフレームを描く

// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
  var nRotationY:Number = mySprite.mouseX * nDeceleration;
  xTransform(vertices, nRotationY);
  var vertices2D:Vector.<Point >  = xGetVertices2D(vertices);
  xDrawLines(vertices2D);
}
function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
  var nLength:uint = myVertices.length;
  var myMatrix3D:Matrix3D = new Matrix3D();
  myMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
  for (var i:int = 0; i<nLength; i++) {
    myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  }
}
function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point >  {
  var vertices2D:Vector.<Point> = new Vector.<Point>();
  var nLength:uint = myVertices.length;
  for (var i:uint = 0; i < nLength; i++) {
    var myVector3D:Vector3D = myVertices[i];
    vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  }
  return vertices2D;
}
function xDrawLines(vertices2D:Vector.<Point>):void {
  var nLength:uint = vertices2D.length;
  var myPoint:Point = vertices2D[nLength - 1];
  myGraphics.clear();
  myGraphics.lineStyle(2, 0x0000FF);
  myGraphics.moveTo(myPoint.x, myPoint.y);
  for (var i:uint = 0; i < nLength; i++) {
    myPoint = vertices2D[i];
    myGraphics.lineTo(myPoint.x, myPoint.y);
  }
}

[ムービープレビュー]を確かめると、マウスポインタの水平位置に応じて正方形のワイヤーフレームが回る。もっとも、不満が残るだろう。パースペクティブがかからないため、回転というより水平に伸び縮みしているように見える（図7⁠）⁠。これは、第33回「遠近法の投影」で触れたDisplayObjectインスタンスに対する処理が、今回の3次元座標を扱うスクリプトには含まれていないからだ。すでに予告したとおり、次回の課題は2次元平面へ座標変換する関数（xGetVertices2D()）に遠近法の投影を加えることだ。

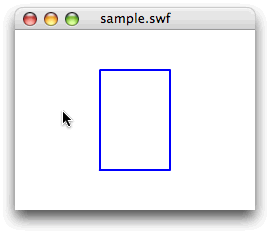
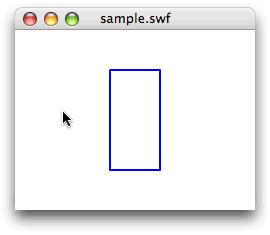
今回解説した次のサンプルファイルがダウンロードできます。

サンプルファイル（CS5形式/約180KB）