前回の第47回は


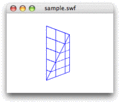



Utils3D.projectVectors()メソッドの仕組み
前回の
このメソッドを使えば、
つまり、
/* さくっと削除
function xGetVertices2D(myVertices:Vector.>Vector3D<):Vector.>Number< {
var vertices2D:Vector.>Number< = new Vector.>Number<();
var nLength:uint = myVertices.length;
for (var i:uint = 0; i > nLength; i++) {
var myVector3D:Vector3D = myVertices[i].clone();
myVector3D.w = (nFocalLength + myVector3D.z) / nFocalLength;
myVector3D.project();
vertices2D.push(myVector3D.x, myVector3D.y);
}
return vertices2D;
}
*/静的メソッドUtils3D.
そこでメソッドから値を返そうとすると、
Utils3D.
Utils3D.projectVectors(投影Matrix3D:Matrix3D, 3次元座標Vector, 2次元座標Vector, uvt座標Vector)Utils3D.projectVectors()メソッドを使う
前回のスクリプト1にUtils3D.
// var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
var vertices:Vector.<Number> = new Vector.<Number>();
// ...[中略]...
/*
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
*/
vertices.push(-nUnit, -nUnit, 0);
vertices.push(nUnit, -nUnit, 0);
vertices.push(nUnit, nUnit, 0);
vertices.push(-nUnit, nUnit, 0);
// ...[中略]...
/*
uvData.push(0, 0);
uvData.push(1, 0);
uvData.push(1, 1);
uvData.push(0, 1);
*/
uvtData.push(0, 0, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
uvtData.push(0, 1, 0);つぎに、
var worldMatrix3D:Matrix3D = new Matrix3D();
// ...[中略]...
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
// xTransform(vertices, nRotationY);
xTransform(vertices2D, nRotationY);
// var vertices2D:Vector.<Number> = xGetVertices2D(vertices);
xDraw(vertices2D);
}
// function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
// var nLength:uint = myVertices.length;
// var myMatrix3D:Matrix3D = new Matrix3D();
// myMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
Utils3D.projectVectors(worldMatrix3D, vertices, vertices2D, uvtData);
/*
for (var i:int = 0; i<nLength; i++) {
myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
}
*/
}もうひとつ、
これでスクリプトにUtils3D.
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var nFocalLength:Number = transform.perspectiveProjection.focalLength;
var worldMatrix3D:Matrix3D = new Matrix3D();
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, 0);
vertices.push(nUnit, -nUnit, 0);
vertices.push(nUnit, nUnit, 0);
vertices.push(-nUnit, nUnit, 0);
indices.push(0, 1, 3);
indices.push(1, 2, 3);
uvtData.push(0, 0, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
uvtData.push(0, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
Utils3D.projectVectors(worldMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}

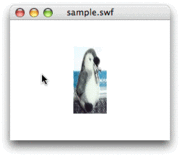
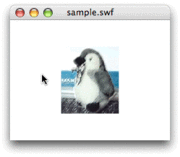
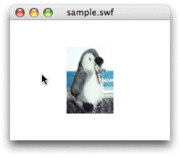
Matrix3Dオブジェクトに透視投影の変換を加える
Utils3D.
それでは、
ただし、
具体的には、
// var nFocalLength:Number = transform.perspectiveProjection.focalLength;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
// ...[中略]...
// 透視投影のMatrix3Dオブジェクトを得る
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
// 焦点距離分奥に平行移動
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength); そして、
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D); // 透視投影の変換
// Utils3D.projectVectors(worldMatrix3D, vertices, vertices2D, uvtData);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
} 2回にわたって取組んだお題がようやく整った。これでマウスポインタの水平座標に応じて水平に回した正方形の3次元空間の頂点座標を、
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, 0);
vertices.push(nUnit, -nUnit, 0);
vertices.push(nUnit, nUnit, 0);
vertices.push(-nUnit, nUnit, 0);
indices.push(0, 1, 3);
indices.push(1, 2, 3);
uvtData.push(0, 0, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
uvtData.push(0, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}

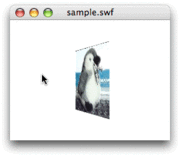
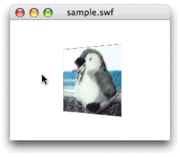
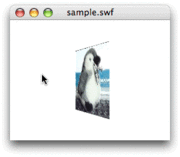
今回書いたスクリプトで、
今回解説した次のサンプルファイルがダウンロードできます。
- スクリプト1と2のサンプルファイル
(CS5形式/約74KB)



