第59回　インスタンスをクリックした点で回しながらドラッグする

今回、目指すお題の動きはこうだった。矩形のインスタンスをドラッグすると、回るように動く。マウスを振り回せば、インスタンスがくるくる回る。そして放すと、滑るように減速して、やがて止まる。どこかで見た覚えのある動きだ。その前編の第57回「インスタンスをクリックした点で回しながらドラッグする」では、ドラッグすると一定の速さで回るところまでできた（第57回スクリプト3⁠）⁠。インスタンスを回すアニメーションのリスナー関数（xDrag()）はつぎに抜書きしたとおりだ。

var lastMouse:Point;
var angularVelocity:Number = 5 * Math.PI / 180;   // 一定値

function xDrag(eventObject:Event):void {
  var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  var myMatrix:Matrix = transform.matrix;
  myMatrix.translate(-lastMouse.x, -lastMouse.y);
  myMatrix.rotate(angularVelocity);   // 回転
  myMatrix.translate(currentMouse.x, currentMouse.y);
  transform.matrix = myMatrix;
  lastMouse = currentMouse.clone();
}

後編の今回は、まずマウスでドラッグする位置と向き、および速さによって回転に加速を与える。そして仕上げは、マウスボタンを放すと、慣性で減速しながらやがて止まるようにする。

ドラッグする位置と向きと速さによって回転を加速する

前編で、インスタンスを回す速さは外積から導くと予告した。外積を求めるには、ベクトルがふたつ要る（図1)。ひとつは、インスタンスの中心、物理でいう重心からドラッグしている座標までのベクトルだ。この距離は離れているほど、回す勢いがつきやすい。つぎに、マウスを動かす速さだ。ただし、その向きも合わせて考えなければならない。ひとつ目のベクトルに対して垂直な力が、インスタンスを回転させる。例によって、物理のもう少し詳しい説明は本稿の最後に行う。

インスタンスのドラッグで回転を加速するアニメーションのリスナー関数（xDrag()）はつぎのようになる。フレームアクション全体は、スクリプト1として後に掲げる。新たに定めた関数（crossProduct2D()）が、ベクトルの外積から回転に用いる値を取出して返す。なお、ベクトルの計算に用いた変数名は、前掲図1に書添えてある。

var lastMouse:Point;
var angularVelocity:Number = 0;
var deceleration:Number = 0.8;
var ratio:Number = 5 / width / height;

function xDrag(eventObject:Event):void {
  var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  var myMatrix:Matrix = transform.matrix;
  var position:Point = new Point(x, y);
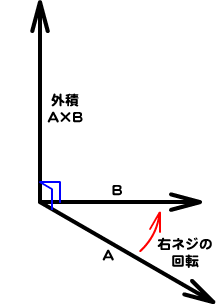
  // 外積を求めるふたつのベクトルの計算
  var radius:Point = lastMouse.subtract(position);
  var force:Point = currentMouse.subtract(lastMouse);
  var moment:Number = crossProduct2D(radius, force);
  angularVelocity += moment * ratio;
  myMatrix.translate(-lastMouse.x, -lastMouse.y);
  myMatrix.rotate(angularVelocity);
  myMatrix.translate(currentMouse.x, currentMouse.y);
  transform.matrix = myMatrix;
  lastMouse = currentMouse.clone();
  angularVelocity *= deceleration;
}
function crossProduct2D(point0:Point, point1:Point):Number {
  var vector0:Vector3D = new Vector3D(point0.x, point0.y, 0);
  var vector1:Vector3D = new Vector3D(point1.x, point1.y, 0);
  var crossProduct3D:Vector3D = vector0.crossProduct(vector1);
  return crossProduct3D.z;
}

ベクトルはPointオブジェクトで定めた。インスタンスの基準点は中心に定めたので、その座標（position）が重心になる。ひとつ目のベクトル（radius）は、ドラッグしている座標（lastMouse）から重心の座標をPoint.subtract()メソッドで差引いて求める。メソッドからは差のベクトルを示すPointインスタンスが返される。ふたつ目のベクトル（force）は、マウスポインタの現在座標（currentMouse）とひとつ前の座標（lastMouse)との差だ。

引かれるPointオブジェクト.subtract(引くPointオブジェクト)

新たに加えた関数（crossProduct2D()）は、渡されたふたつのPointオブジェクトをVector3Dインスタンスに直したうえで、Vector3D.crossProduct()メソッドによりふたつのベクトルの外積（crossProduct3D）を求める。そして、外積のVector3Dオブジェクトからz座標値（Vector3D.zプロパティ）を取出して返している。ドラッグするインスタンスの回転は、この戻り値（moment）に比例して加速させる。

ただし、外積の大きさはふたつのベクトルの長さの積をもとに計算される。他方で、角度のラジアン値はわずか3.14で1周してしまう。数値の違いが大きすぎるので、調整用の係数を変数（ratio)に定めた。そして、前述関数（crossProduct2D()）の戻り値（moment）にこの係数を乗じたうえで、回転角（angularVelocity）に加速度として加えた。

これで、インスタンスをドラッグする位置と方向、およびその大きさによって回転が加速される（図2⁠）⁠。もっとも、加速しっ放しではまずい。減速の係数も定め（deceleration⁠）⁠、リスナー関数（xDrag())の最後で回転角（angularVelocity）に乗じた。フレームアクション全体は、つぎのスクリプト1のとおりだ。

スクリプト1　インスタンスをドラッグで加速して回す

// フレームアクション: マウスでドラッグして回すMovieClipシンボル
var lastMouse:Point;
var angularVelocity:Number = 0;
var deceleration:Number = 0.8;
var ratio:Number = 5 / width / height;
addEventListener(MouseEvent.MOUSE_DOWN, xMouseDown);
function xMouseDown(eventObject:MouseEvent):void {
  lastMouse = new Point(parent.mouseX, parent.mouseY);
  addEventListener(Event.ENTER_FRAME, xDrag);
  stage.addEventListener(MouseEvent.MOUSE_UP, xMouseUp);
}
function xMouseUp(eventObject:MouseEvent):void {
  removeEventListener(Event.ENTER_FRAME, xDrag);
  stage.removeEventListener(MouseEvent.MOUSE_UP, xMouseUp);
}
function xDrag(eventObject:Event):void {
  var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  var myMatrix:Matrix = transform.matrix;
  var position:Point = new Point(x, y);
  var radius:Point = lastMouse.subtract(position);
  var force:Point = currentMouse.subtract(lastMouse);
  var moment:Number = crossProduct2D(radius, force);
  angularVelocity += moment * ratio;
  myMatrix.translate(-lastMouse.x, -lastMouse.y);
  myMatrix.rotate(angularVelocity);
  myMatrix.translate(currentMouse.x, currentMouse.y);
  transform.matrix = myMatrix;
  lastMouse = currentMouse.clone();
  angularVelocity *= deceleration;
}
function crossProduct2D(point0:Point, point1:Point):Number {
  var vector0:Vector3D = new Vector3D(point0.x, point0.y, 0);
  var vector1:Vector3D = new Vector3D(point1.x, point1.y, 0);
  var crossProduct3D:Vector3D = vector0.crossProduct(vector1);
  return crossProduct3D.z;
}

マウスボタンを放したら慣性で減速しながら移動する

仕上げは、マウスボタンを放したときの慣性の動きだ。最後にドラッグした向きに、インスタンスを減速しながら移動する。そのためには、マウスボタンが放されたら、DisplayObject.enterFrameイベントからドラッグのリスナー関数（xDrag()）を除くと同時に、慣性で移動するリスナー関数に差替えることになる。前掲フレームアクション（スクリプト1）に加える処理は以下のようになる。全体はスクリプト2として後に掲げた。

慣性で移動するリスナー関数（xThrow()）は、ドラッグで回すアニメーションのリスナー関数（xDrag()）を少し手直しすればよい。第1に、もはや回転の加速はない。次第に回り方は遅くなる。逆に第2として、ドラッグはなくなっても、慣性でインスタンスが移動する。直前のマウスドラッグを慣性のベクトル（velocity）として保持し、その方向に動き続ける。ただし、回転と同じ減速率（deceleration）を乗じるので、やがて止まる。

var velocity:Point;

function xMouseUp(eventObject:MouseEvent):void {
  // ...[中略]...
  addEventListener(Event.ENTER_FRAME, xThrow);
}

function xDrag(eventObject:Event):void {
  // ...[中略]...
  velocity = force;
}

function xThrow(eventObject:Event):void {
  var myMatrix:Matrix = transform.matrix;
  myMatrix.translate(-x, -y);
  myMatrix.rotate(angularVelocity);
  myMatrix.translate(x + velocity.x, y + velocity.y);
  transform.matrix = myMatrix;
  velocity.normalize(velocity.length * deceleration);
  angularVelocity *= deceleration;
  if (Math.abs(angularVelocity) < 0.1 && velocity.length < 0.1) {
    removeEventListener(Event.ENTER_FRAME, xThrow);
  }
}

少し細かい処理を補っておこう。慣性で動くとき、ドラッグはされていないので、回転の中心はインスタンスの基準点にした。そのため、回す前に移動するMatrix.translate()メソッドにはインスタンスの座標をマイナスにした値（-x, -y）が渡されている。そして、回転の後の移動は、慣性のベクトル（velocity）の（x, y）座標を加えた。

慣性のベクトル（velocity）の減速は、Point.normalize()メソッドで長さを縮めた。つまり引数には、もとのベクトルの長さ（Point.lengthプロパティ）に減速率を乗じた値を渡している。リスナー関数の締めは、回転角（angularVelocity）と慣性ベクトル（velocity）の長さが十分小さくなったことを確かめたうえで、イベントから削除する。これでインスタンスのアニメーションが完全に終わる。でき上がったフレームアクション全体は、つぎのスクリプト2のとおりだ。

スクリプト2　ドラッグで回転してボタンを放すと慣性で移動する

// フレームアクション: マウスでドラッグして回すMovieClipシンボル
var lastMouse:Point;
var angularVelocity:Number = 0;
var velocity:Point;
var deceleration:Number = 0.8;
var ratio:Number = 5 / width / height;
addEventListener(MouseEvent.MOUSE_DOWN, xMouseDown);
function xMouseDown(eventObject:MouseEvent):void {
  lastMouse = new Point(parent.mouseX, parent.mouseY);
  addEventListener(Event.ENTER_FRAME, xDrag);
  stage.addEventListener(MouseEvent.MOUSE_UP, xMouseUp);
}
function xMouseUp(eventObject:MouseEvent):void {
  removeEventListener(Event.ENTER_FRAME, xDrag);
  stage.removeEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  addEventListener(Event.ENTER_FRAME, xThrow);
}
function xDrag(eventObject:Event):void {
  var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  var myMatrix:Matrix = transform.matrix;
  var position:Point = new Point(x, y);
  var radius:Point = lastMouse.subtract(position);
  var force:Point = currentMouse.subtract(lastMouse);
  var moment:Number = crossProduct2D(radius, force);
  angularVelocity += moment * ratio;
  myMatrix.translate(-lastMouse.x, -lastMouse.y);
  myMatrix.rotate(angularVelocity);
  myMatrix.translate(currentMouse.x, currentMouse.y);
  transform.matrix = myMatrix;
  lastMouse = currentMouse.clone();
  angularVelocity *= deceleration;
  velocity = force;
}
function xThrow(eventObject:Event):void {
  var myMatrix:Matrix = transform.matrix;
  myMatrix.translate(-x, -y);
  myMatrix.rotate(angularVelocity);
  myMatrix.translate(x + velocity.x, y + velocity.y);
  transform.matrix = myMatrix;
  velocity.normalize(velocity.length * deceleration);
  angularVelocity *= deceleration;
  if (Math.abs(angularVelocity) < 0.1 && velocity.length < 0.1) {
    removeEventListener(Event.ENTER_FRAME, xThrow);
  }
}
function crossProduct2D(point0:Point, point1:Point):Number {
  var vector0:Vector3D = new Vector3D(point0.x, point0.y, 0);
  var vector1:Vector3D = new Vector3D(point1.x, point1.y, 0);
  var crossProduct3D:Vector3D = vector0.crossProduct(vector1);
  return crossProduct3D.z;
}

回転の加速と減速の度合いは変数（ratioとdeceleration）に定めたので、希望の動きになるよう調整してほしい。外積を用いた回転の加速度の求め方（関数crossProduct2D()）について、原理はあまり説明しなかった。このお題の結びとして、次項に物理の解説を加える（苦手な読者は読み飛ばしてもらって構わない⁠）⁠。

剛体を回す力の働き－力のモーメント

かたちの変わらない固いもの（⁠「⁠剛体」という）を回転させるとき、その力のかかり具合は「力のモーメント」という考え方で表される。柄の細いドライバーと太いドライバーとでは、同じ力を加えてもねじの回しやすさが変わる。その回しやすさが、力と区別された力のモーメントなのだ。

太いドライバに力が加えやすいのは、てこの原理が働くからだ（図3⁠）⁠。インスタンスを回転する場合でいえば、重心（中心）が支点でドラッグするマウスポインタの位置が力点になる。その2点を結ぶペクトルに対して垂直に加えた力（動き）が、インスタンスを回すことになる。

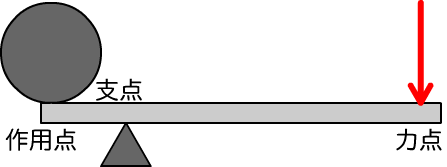
力がてこ（支点から力点を結ぶベクトル）に対して垂直でない場合、その力のベクトルを対角線とする平行四辺形（長方形を含む）を描けば、その2辺でふたつのベクトルに分けることができる（図4⁠）⁠。てこに加えられた力（F)も、てこに平行（F_//）と垂直（F_⊥）のふたつのベクトルに分けられる。

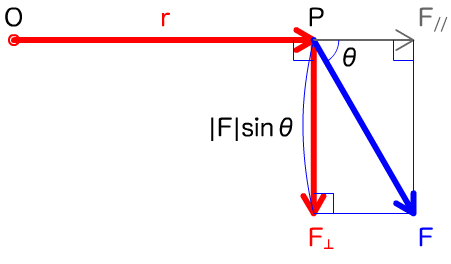
インスタンスを回転する働きは、その垂直の力の大きさ（|F|sinθ）に比例する。そして、てこはもちろんその長さ（|r|）に応じて、力がかかりやすくなる。つまり、これらふたつの大きさの積（|r||F|sinθ）に比例して、回転の加速度が増すということだ。この積は、ふたつのベクトル（rとF）を2辺とする平行四辺形の面積に等しい。

ここで、ベクトルの外積を思い出そう（第52回「ベクトルの外積で回転の軸を定める」参照)。ふたつのベクトルの外積（A×B）の大きさが、まさにふたつのベクトルを2辺とする平行四辺形の面積（|A||B|sinθ）で定められていた（第52回表1再掲⁠）⁠。

外積の要素	求められた外積のベクトルとふたつのベクトルAとBとの関係
方向	角度	ふたつのベクトルAとBのどちらにも垂直
向き	ベクトルAからBに向かう回転で右ネジの進む向き
大きさ	\|A\|\|B\|sinθ

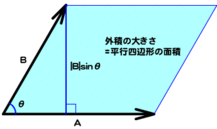
外積はふたつのベクトルのどちらにも垂直なベクトルだった。つまり、xy平面上のふたつのベクトルの外積は、z軸に平行なベクトルになる。それは、外積のベクトルのxy座標が、つねに0であることを意味する。そのため、前掲スクリプト2で外積を用いた関数（crossProduct2D()）では、外積のベクトル（crossProduct3D）のz座標値だけ取出して返している。

もっとも、関数の返すz座標値は、引数に受取ったふたつのベクトル（point0とpoint1）が右ネジの位置にあるかそうでないかで、正負は逆になる。すると、インスタンスを回す角度の向きが変わるのである。このようにして外積を使うことにより、マウスでドラッグするインスタンスの位置と向き、および大きさから、回転する加速度とその方向が導けるのだ[1]⁠。

Flash Professional CS6が発表された。そこでこの本編のつぎ（第61回）からは、Flash Player 11に備わったStage3Dにもとづく2次元フレームワークStarlingを扱う。

今回解説した次のサンプルファイルがダウンロードできます。

スクリプト1～2のサンプルファイル（CS5形式/約98KB）

ドラッグする位置と向きと速さによって回転を加速する

マウスボタンを放したら慣性で減速しながら移動する

剛体を回す力の働き － 力のモーメント

剛体を回す力の働き－力のモーメント