はじめに
前々回、
前回の復習
まず、
- イベントは、
線分の始点と終点、 そして交点に対応するオブジェクトです。前回は、 イベントを表現するEventクラスを作成しました。 - イベントキューは、
イベントを要素とするコレクションです。キューの要素は、 イベント点のy座標が小さい順に、 常にソートされています。前回、 イベントキューには、 java. util. TreeSetクラスを利用することを説明しました。 - ステータスは、
現在の走査線と交わる線分を要素とするコレクションです。ステータスの要素は、 走査線と線分の交点のx座標が小さい順に、 常にソートされています。ステータスにもTreeSetクラスを利用します。
この3つを使って交差検出のアルゴリズムを組み立てることが、
イベントの処理
イベントキューには、
さて、
始点イベントの処理
始点イベントをきっかけとして、
さらにこのとき、
- ステータス中でSstartの直前
(左隣) に位置する線分 (Sl) - ステータス中でSstartの直後
(右隣) に位置する線分 (Sr)
もし交差する場合には、
図1は始点イベントの例です。この図の場合、
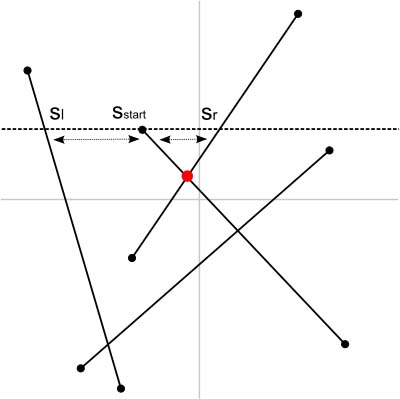
交点イベントの処理
交点イベントには、
交点を境にして、
このとき、
- 元のステータス中でS'lの直前
(左隣) に位置した線分とS'r - 元のステータス中でS'rの直後
(右隣) に位置した線分とS'l
それぞれ、

終点イベントの処理
走査線が終点イベントに着くと、
ここで、
- ステータス中でSendの直前
(左隣) に位置する線分 (S''l) - ステータス中でSendの直後
(右隣) に位置する線分 (S''r)
S''lとS''rはこれまで、

以上をまとめると、
| 種類 | ステータスの変更 | 交差チェック対象 |
|---|---|---|
| 始点 | 線分を挿入 | 挿入した線分とその左隣/ |
| 交点 | 2線分の位置を交換 | 新しく左に来る線分とその左隣/ |
| 終点 | 線分を削除 | 削除する線分の左隣と右隣 |
平面走査法の実装
それでは、
public class PlaneSweepIntersectionDetector implements IntersectionDetector {
public Collection<Intersection> execute(List<LineSegment> segments) {
// イベントキューを作成
TreeSet<Event> eventQueue = new TreeSet<Event>();
for (LineSegment s : segments) {
// 線分の端点のうち上にある方を始点、下にある方を終点としてイベントを登録
// 線分が水平な場合は左の端点を始点とする
if (s.y1 < s.y2 || (s.y1 == s.y2 && s.x1 < s.x2)) {
eventQueue.add(new Event(Event.Type.SEGMENT_START, s.x1, s.y1, s, null));
eventQueue.add(new Event(Event.Type.SEGMENT_END, s.x2, s.y2, s, null));
} else {
eventQueue.add(new Event(Event.Type.SEGMENT_START, s.x2, s.y2, s, null));
eventQueue.add(new Event(Event.Type.SEGMENT_END, s.x1, s.y1, s, null));
}
}
SweepLineBasedComparator sweepComparator = new SweepLineBasedComparator();
// ステータスを作成。要素の順序関係はsweepComparatorにしたがう
TreeSet<LineSegment> status = new TreeSet<LineSegment>(sweepComparator);
// 今回の実装では同一の交点が複数回検出される可能性があるため、HashSetを使って重複を防ぐ
Collection<Intersection> result = new HashSet<Intersection>();
Event event;
// キューから先頭のイベントを取り出す
while ((event = eventQueue.pollFirst()) != null) {
double sweepY = event.y;
switch (event.type) {
case SEGMENT_START: // 始点イベントの場合
sweepComparator.setY(sweepY); // 走査線を更新
LineSegment newSegment = event.segment1;
status.add(newSegment); // ステータスに線分を追加
LineSegment left = status.lower(newSegment);
LineSegment right = status.higher(newSegment);
// 左隣の線分との交差を調べる
checkIntersection(left, newSegment, sweepY, eventQueue);
// 右隣の線分との交差を調べる
checkIntersection(newSegment, right, sweepY, eventQueue);
break;
case INTERSECTION: // 交点イベントの場合
left = event.segment1;
right = event.segment2;
// 交点を戻り値に追加
result.add(new Intersection(left, right));
LineSegment moreLeft = status.lower(left);
LineSegment moreRight = status.higher(right);
// ステータス中のleftとrightの位置を交換するため、いったん削除する
status.remove(left);
status.remove(right);
sweepComparator.setY(sweepY); // 走査線を更新
// 計算誤差により、走査線の更新後も順序が交換されない場合は
// 走査線を少し下げて順序が確実に変わるようにする
if (sweepComparator.compare(left, right) < 0) {
sweepComparator.setY(sweepY + 0.001);
}
// 更新後の走査線を基準としてleftとrightを再追加(位置が交換される)
status.add(left);
status.add(right);
// right(位置交換によって新しく左側に来た線分)と、そのさらに左隣の線分の交差を調べる
checkIntersection(moreLeft, right, sweepY, eventQueue);
// left(位置交換によって新しく右側に来た線分)と、そのさらに右隣の線分の交差を調べる
checkIntersection(left, moreRight, sweepY, eventQueue);
break;
case SEGMENT_END: // 終点イベントの場合
LineSegment endSegment = event.segment1;
left = status.lower(endSegment);
right = status.higher(endSegment);
// 線分の削除によって新しく隣り合う2線分の交差を調べる
checkIntersection(left, right, sweepY, eventQueue);
status.remove(endSegment); // ステータスから線分を削除
sweepComparator.setY(sweepY); // 走査線を更新
break;
}
}
return result;
}
// 線分leftとrightが走査線の下で交差するかどうか調べ、交差する場合は交点イベントを登録する
private void checkIntersection(LineSegment left, LineSegment right,
double sweepY, TreeSet<Event> eventQueue) {
// 2線分のうち少なくとも一方が存在しない場合、何もしない
if (left == null || right == null) {
return;
}
Point2D p = left.getIntersectionPoint(right);
// 交点が走査線よりも下に存在するときのみ、キューに交点イベントを登録
if (p != null && p.getY() >= sweepY) {
eventQueue.add(new Event(Event.Type.INTERSECTION, p.getX(), p
.getY(), left, right));
}
}
}プログラムではまず、
ただし、
平面走査法の計算量
平面走査法による線分交差検出の計算量は、
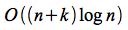
で表されます。交点数に依存した計算量となるため、
デモプログラム
今回解説したアルゴリズムをグラフィカルに動作確認できるよう、
デモプログラムを起動すると、
まとめと次回予告
今回は、
今回作成したプログラムのソースコードがダウンロードできます。
- 第5回ソースコードファイル
(gihyo-geometry-part5. zip/ Zip圧縮/約90KB)
次回からは、



