はじめに
前回に引き続き、平面走査法のアプローチを用いて、2つの凸多角形の交差部分を求める方法を解説します。今回は、まずWeb上で実行可能なデモプログラムを示した上で、プログラムを実際に操作しながら、その動きを追うかたちで説明を行います。
前回の復習
最初に、前回のポイントを押さえておきましょう。
- 2つの凸多角形の交差部分は、同じく凸多角形になる
- 2つの凸多角形の交差計算には、第3回~第5回で解説した平面走査法を応用できる
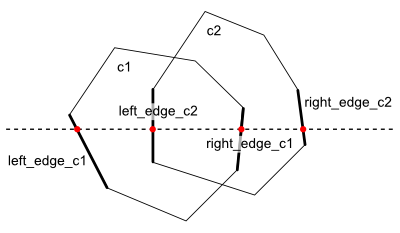
- 走査線と交わる線分は、left_edge_c1, right_edge_c1, left_edge_c2, right_edge_c2のたかだか4個である(図1)
- イベント点となるのは、入力の凸多角形の頂点のみである
- left_edge_c1, right_edge_c1, left_edge_c2, right_edge_c2の4辺の各終点のうち、もっとも上にある点が次のイベント点になる
図1 走査線と交わる4辺
交差計算のデモプログラム
それでは早速、デモプログラムを示します。
このリンクをクリックしてください。Java Web Start形式のプログラムが起動します。これは、平面走査法による凸多角形の交差計算過程を、グラフィックで段階的に表示するデモになっています。
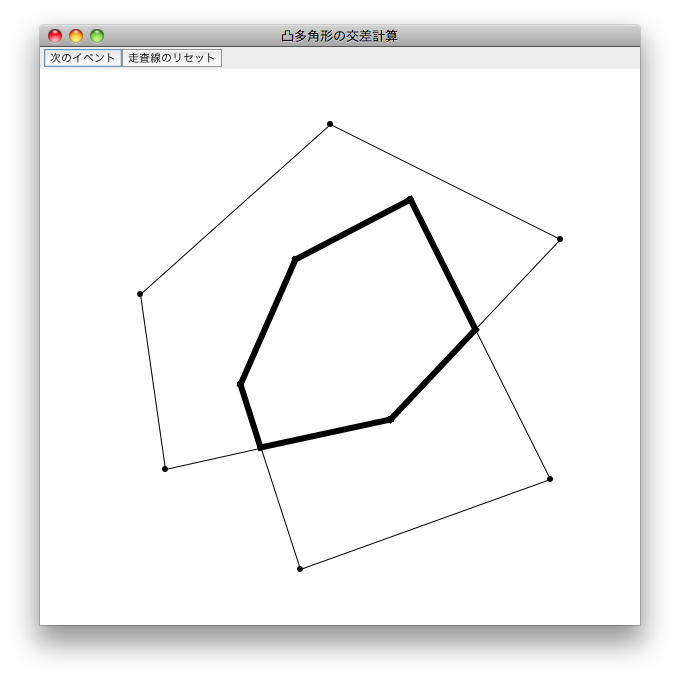
ウィンドウの中には、2つの凸多角形が置かれています(図2)。辺や頂点をドラッグすると、図形を移動したり、変形したりすることができます。ただし、凸でない多角形にすることはできません。
図2 デモプログラムを起動したところ
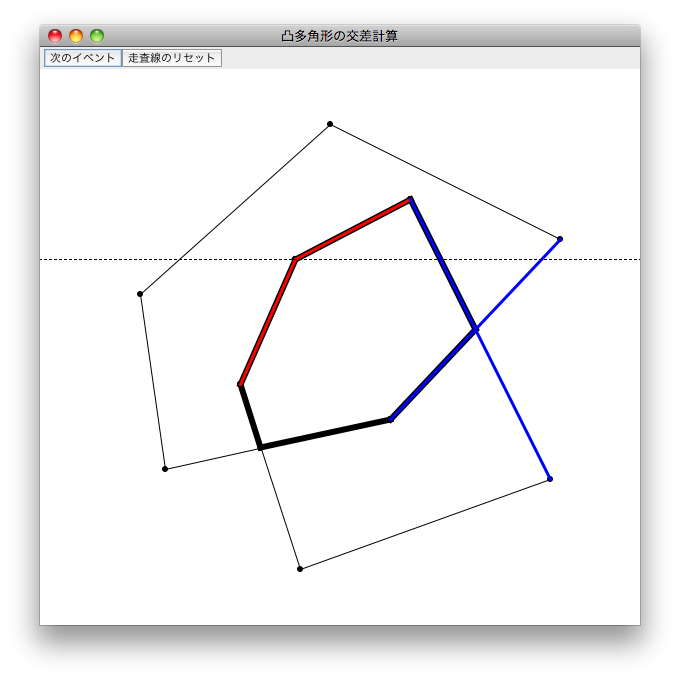
画面上部の「次のイベント」ボタンをクリックすると、特定の頂点位置に走査線が現れます。さらに続けて「次のイベント」ボタンをクリックすると、走査線が少しずつ下に移動していきます。走査線が移動する過程で、2つの多角形の交差部分となる辺が、順に赤色と青色で塗られていきます(図3)。赤色は、交差計算結果となる凸多角形の「左側」の辺を示し、青色は「右側」の辺を示しています。計算がすべて終わり、交差部分の凸多角形が確定すると、走査線は消滅します。
図3 交差部分の辺検出過程
2つの凸多角形をいろいろな配置に変えて、走査線がどのような動きをするか、そして交差部分の辺がどのように決まっていくかを確認してみてください。
走査線の開始位置
では最初の問題として、走査線がどの頂点位置からスタートしているかを観察してください。いろいろと条件を変えて試すと分かりますが、これは入力となる2つの凸多角形のうち、より下にある方の最上端の頂点になっています(図4)。
図4 走査線の開始位置
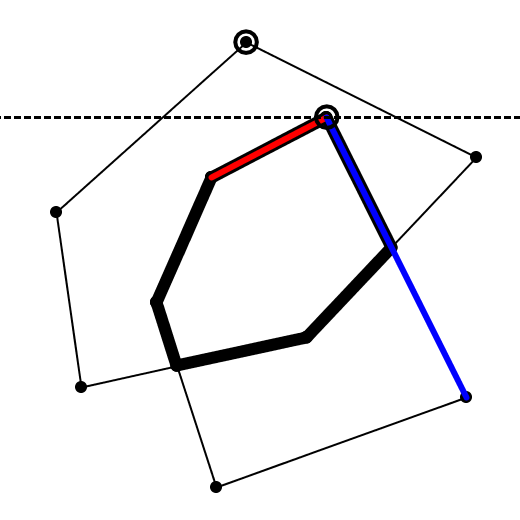
この位置は、2つの凸多角形が同時に存在し得るy座標の上限です。ここより上には片方の多角形しかないので、交差領域は絶対に存在しないことになります。
イベントの処理(開始辺がleft_edge_c1の場合)
次に、イベントの具体的な処理を見ていきましょう。イベント点から新しく始まる辺が、left_edge_c1, right_edge_c1, left_edge_c2, right_edge_c2のうちどれにあたるかによって、処理の内容は異なりますが、ここでは、left_edge_c1の場合について考えます(条件が重複して成立することもあるので注意してください)。
条件1:left_edge_c1がleft_edge_c2とright_edge_c2の間にあるとき(図5)
図5 left_edge_c1がleft_edge_c2とright_edge_c2の間にあるとき
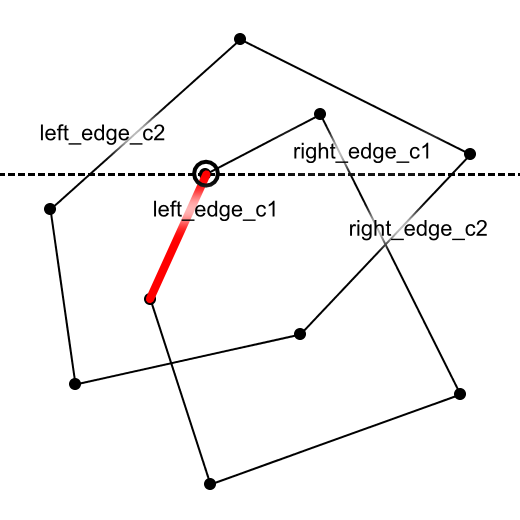
このとき、left_edge_c1は必ず、交差領域の左側を構成します。したがって、計算結果にleft_edge_c1を追加します。
条件2 left_edge_c1がright_edge_c2より右から始まり、right_edge_c2と交わるとき(図6)
図6 left_edge_c1がright_edge_c2より右から始まり、right_edge_c2と交わるとき
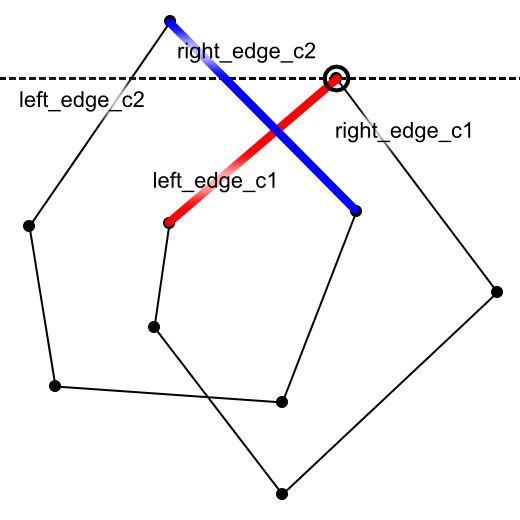
このとき、left_edge_c1とright_edge_c2の両方が交差領域を構成します。したがって、計算結果にleft_edge_c1とright_edge_c2の両方を追加します。なお、このとき、left_edge_c1とright_edge_c2の交点が、交差領域の最上端になります。
条件3、条件4:left_edge_c1がleft_edge_c2と交わるとき
このときは、2つの可能性があります。
条件3: left_edge_c1がleft_edge_c2と交わり、かつleft_edge_c2より右から始まるとき(図7)
図7 left_edge_c1がleft_edge_c2と交わり、かつleft_edge_c2より右から始まるとき
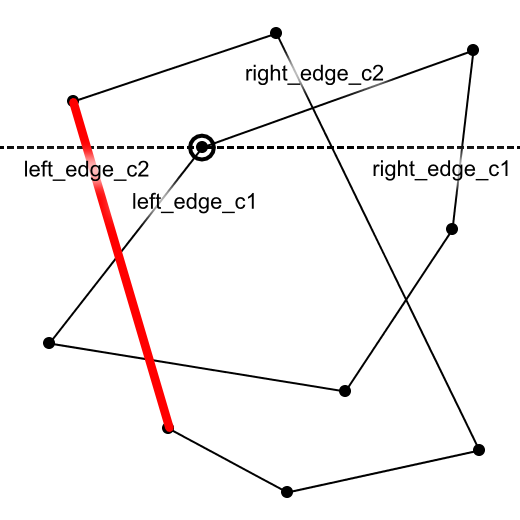
この場合、left_edge_c2は交差領域を構成します。したがって、計算結果にleft_edge_c2を追加します。図7を見ると、left_edge_c1も交差領域の一部では?と思うかもしれませんが、この図のleft_edge_c1は条件1に該当するため、すでに計算結果に追加済みです。
条件4: left_edge_c1がleft_edge_c2と交わり、かつleft_edge_c2より左から始まるとき(図8)
図8 left_edge_c1がleft_edge_c2と交わり、かつleft_edge_c2より左から始まるとき
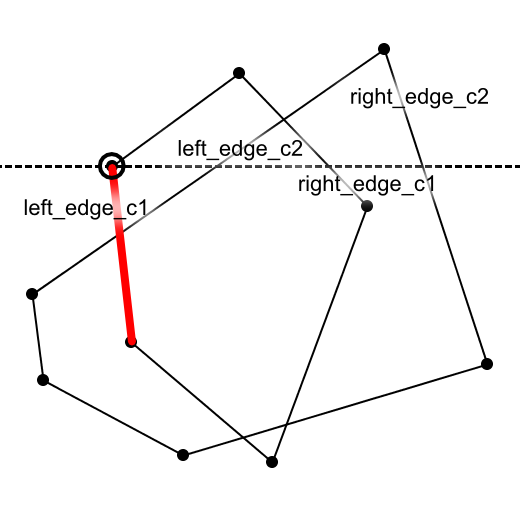
この場合、left_edge_c1は交差領域を構成します。したがって、計算結果にleft_edge_c1を追加します。
以上が、イベント点から始まる辺がleft_edge_c1のケースにおける処理のすべてになります。条件1から4のいずれも、ステータス上の他の辺との位置関係から判定が可能です。
イベントの処理(開始辺がその他の場合)
イベント点から始まる辺がleft_edge_c1の場合について見てきましたが、right_edge_c1, left_edge_c2, right_edge_c2の場合はどうなるでしょうか。今回のアルゴリズムには対称性がありますので、left_edge_c1の場合の処理と同様に考えることができます。以下、例としてright_edge_c1の場合を示します。
条件1:right_edge_c1がleft_edge_c2とright_edge_c2の間にあるとき
計算結果にright_edge_c1を追加します。
条件2 right_edge_c1がleft_edge_c2より左から始まり、left_edge_c2と交わるとき
計算結果にright_edge_c1とleft_edge_c2の両方を追加します。
条件3:right_edge_c1がright_edge_c2と交わり、かつright_edge_c2より左から始まるとき
計算結果にright_edge_c2を追加します。
条件4:right_edge_c1がright_edge_c2と交わり、かつright_edge_c2より右から始まるとき
計算結果にright_edge_c1を追加します。
走査完了時の処理
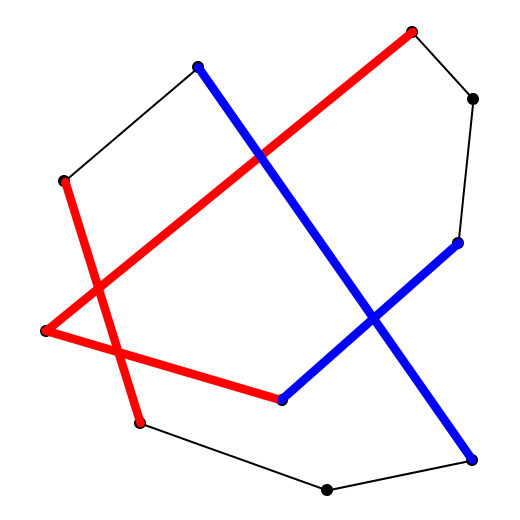
ここまでの手順で交差領域を形成する辺がすべて検出され、これ以上走査線を動かせなくなったとき、イベントの処理は完了します。ただしこの時点では、結果は元の多角形における左右の辺リストとして表現されており、まだ凸多角形の形式になっていません(図9)。
図9 イベント処理完了時点の計算結果
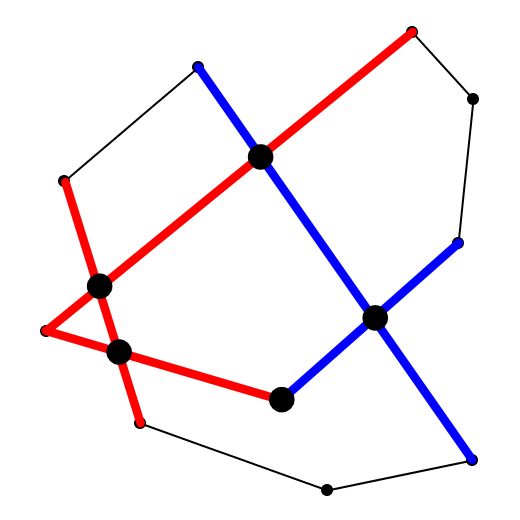
そこで、このリストの中で、隣接する辺同士の交点を求めます(図10)。これらの交点を結ぶと、交差領域の凸多角形が完成します。
図10 隣接する辺同士の交点
いかがだったでしょうか。平面走査法のアプローチによって、2つの凸多角形の交差領域を高速に計算できることが分かったと思います。デモプログラムをもう一度動かして、ここまで説明した処理内容を1つずつ確認してみてください。
まとめと次回予告
今回は、デモプログラムを使いながら、平面走査法を使った凸多角形の交差計算のアルゴリズムを解説しました。実際のプログラムがどうなっているか興味を持った方は、ぜひ以下からソースコードをダウンロードして、実装に目を通してみてください。
今回作成したプログラムのソースコードは、こちらからダウンロードできます。
次回からは、いよいよ本連載最後のトピックとして、ボロノイ図の作成に挑戦します。お楽しみに!













