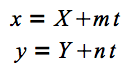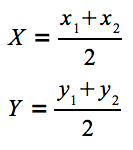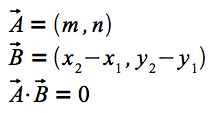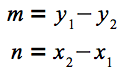はじめに

本連載では、ごく単純な直線の式からスタートし、線分、多角形とステップアップしながら計算幾何を学習してきました。その最後の締めくくりとして、今回からは、ボロノイ図の作成方法を見ていくことにします。

ボロノイ図とは

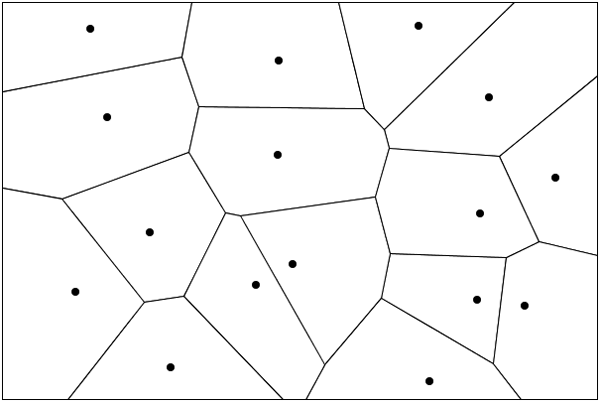
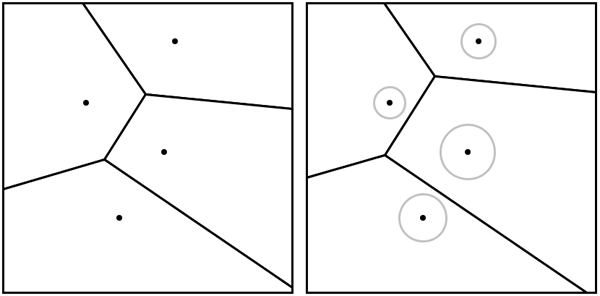
まず、第1回でも簡単に触れたボロノイ図について、改めて説明します。 平面上に複数の母点が配置されているとき、それぞれの母点に最も近くなる点を集めると、母点ごとに「勢力図」のような領域が形成されます。この領域分割図をボロノイ図（voronoi diagram）といいます（図1⁠）⁠。

ボロノイ図の各領域をボロノイ領域（voronoi region）と呼び、ボロノイ領域の境界線をボロノイ辺（voronoi edge）と呼びます。

ボロノイ辺の性質

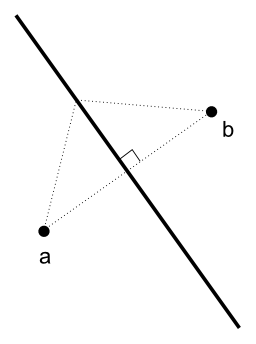
ボロノイ図において、ボロノイ辺が持つ性質を考えてみましょう（図2⁠）⁠。

母点aと母点bを隔てるボロノイ辺から少しでもaに向かって移動すると、その地点はbよりもaに近くなります。同様に、辺から少しでもbに向かって移動すると、その地点はaよりもbに近くなります。したがって、aとbを隔てるボロノイ辺は、aとbからちょうど距離の等しい点を集めた直線になることが分かります。すなわち、これはaとbの垂直二等分線（perpendicular bisector）ということになります。

ボロノイ図と最近傍探索

ボロノイ図は計算幾何学の代表的なテーマの1つであり、その応用範囲は多岐にわたります。1つの例として、最近傍探索（nearest neighbor search）問題を紹介しましょう。

ドライブ中にガソリンが少なくなったとき、最寄りのガソリンスタンドはどのようにして見つければ良いでしょうか。このように、点集合の中から最も近い点を探し出す問題を最近傍探索といいます。

解の候補を母点とするボロノイ図をあらかじめ作成しておくと、最近傍探索問題を高速に解くことができます。

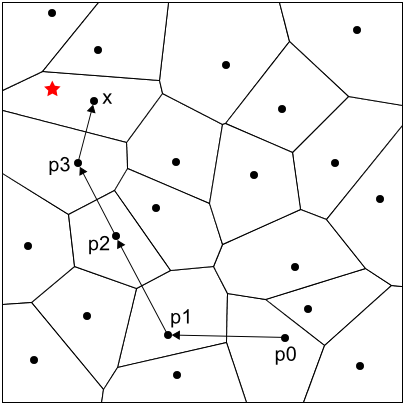
図3において、赤い星印からもっとも近い母点を探すには、まず、適当な母点p0を選びます。次に、p0と隣接する母点のうち、星印にもっとも近くなる母点p1を見つけます。このようにして母点を辿っていくと、解である母点xに高速に到達することができます。

ボロノイ図とBlogopolis

もう1つ、ボロノイ図の応用例として、筆者の開発したBlogopolisを挙げてみたいと思います。

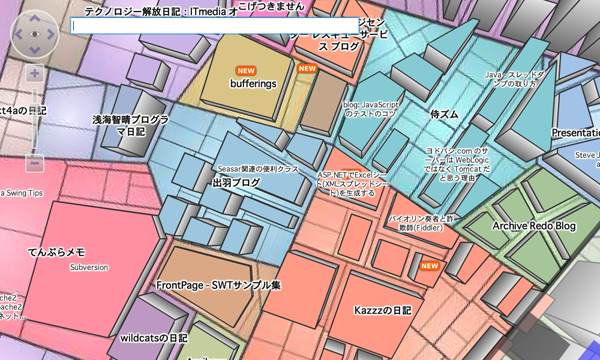
Blogopolisは、ブロガーがそのブックマーク獲得数に応じた大きさの「土地」を持っており、その土地に各ブログ記事を表す「ビル」が建つという構造になっています。この「土地」と「ビル」の区画分けのうち、前者にボロノイ図が使われています。

Blogopolisで使用しているボロノイ図は、加法的重み付きべき乗ボロノイ図（additively weighted power voronoi diagram）と呼ばれるものです。これは、通常のボロノイ図と少し異なり、各母点に重み（weight）が与えられ、母点の距離関数が重みの影響を受けるようになっています。その結果として、各ボロノイ辺が本来の垂直二等分線の位置から平行移動します（図5⁠）⁠。

図5の左右を比較すると、大きな重み（円の大きさで示されています）を持つ母点のボロノイ領域が、小さな重みの領域を「押しのけて」いる様子が分かると思います。Blogopolisでは、この重みを適切に設定することで、ボロノイ領域の面積比を意図的に操作し、ブロガーのブックマーク獲得数の比率に一致させているわけです。

半平面交差にもとづくボロノイ図の作成

それでは、ボロノイ図を作成する具体的なアルゴリズムを考えていきましょう。今回は、直感的に理解しやすく実装も容易な、半平面交差にもとづく方法を取り上げます（本連載では扱いませんが、より高度なアルゴリズムとして、平面走査法にもとづくFortuneのアルゴリズムと呼ばれる手法もあります⁠）⁠。

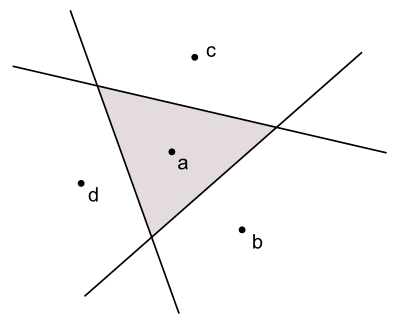
図6を見てください。母点aを母点b, c, dが取り囲んでいるとき、母点aのボロノイ領域はどのような形状になるでしょうか。容易に分かるように、これは、aとb、aとc、aとdそれぞれの垂直二等分線で囲まれた三角形です。

このことは、次のように言い換えることができます。aとbの垂直二等分線によって作り出される2つの半平面（half plane）のうち、aを含む方の半平面をh(a, b)とおきます。同様に、半平面h(a, c)とh(a, d)を考えます。すると、母点aのボロノイ領域は、h(a, b), h(a, c), h(a, d)の3つの半平面の共通部分、すなわち交差領域として求めることができます。

母点の数がどれだけ増えても、この考え方はそのまま適用可能です。ある母点のボロノイ領域は、その母点と他の各母点の垂直二等分線から作られる半平面の交差領域となるのです。

さて、前々回、前回と、凸多角形同士の交差領域を計算する方法を学習してきたので、これをうまく流用することを考えます。半平面は無限に広がる領域ですが、その平面分割線を辺として持つ十分に大きな凸多角形を作れば、その凸多角形は実用上、半平面と見なすことができます。したがって、半平面から凸多角形への変換作業を行うことで、凸多角形の交差計算のアルゴリズムをそのまま用い、半平面の交差領域が求められることになります。

垂直二等分線の計算

半平面を凸多角形に置き換える方法は次回に譲ることにして、今回はまず、垂直二等分線の計算を実装しておきます。

点p₁の座標を(x₁, y₁)、点p₂の座標を(x₂, y₂)とするとき、p₁とp₂の垂直二等分線の方程式を求めてみましょう。

垂直二等分線を次のように媒介変数表示してみます。

垂直二等分線はp₁とp₂の中点を通るので、上の式において

となります。

次に、mとnの値を求めます。垂直二等分線と、p₁とp₂を結ぶ直線は直交するので、この2つの直線から作った2つのベクトルの内積はゼロになるはずです。すなわち

となり、これを計算すると、mとnを例えば次のように決めることができます。

以上で媒介変数表示が完成したので、tに適当な値を2つ（例えば0と1）代入して、垂直二等分線が通る2点を求めます。この2点を前回までの連載で実装済みのLine#fromPoints()メソッドに渡すことで、直線オブジェクトを作成できます。

それでは、この方針にもとづき、LineクラスにperpendicularBisector()メソッドを追加してみましょう。

public static Line perpendicularBisector(double x1, double y1,
        double x2, double y2) {
    double cx = (x1 + x2) / 2.0;
    double cy = (y1 + y2) / 2.0;
    return fromPoints(cx, cy, cx + (y1 - y2), cy + (x2 - x1));
}

次回以降、この垂直二等分線をもとに半平面を生成し、ボロノイ図の作成へと進んでいきます。

まとめと次回予告

今回は、本連載最後のトピックとして、ボロノイ図の説明を行いました。ボロノイ辺が母点の垂直二等分線になっているという性質を示し、ボロノイ図の作成の準備段階として、2点の座標から垂直二等分線を求めるコードを実装しました。

今回作成したプログラムのソースコードは、こちらからダウンロードできます。

次回は、凸多角形の交差計算アルゴリズムを利用して半平面の交差領域を求め、ボロノイ領域を計算する段階へと入っていきます。お楽しみに！