ものづくりには規格が必要です。「規格」と聞くとルールに縛られるイメージがあります。しかし、ものづくりにおける規格は、私たちを余計な作業から自由にします。
規格が私たちを助けてくれる身近な例は「ねじ」です。日本にはJIS（日本工業規格）があります。JISにそって作られた同じ規格の雄雌のねじは、どの会社が作ったものでも互いにかみ合います。もしそうでなかったら、ひとつの会社の作った部品しか使えなくなります。
規格があるというのは、ある程度規格のことを知る手間がかかるデメリットを考えても、大変有利なことなのです。ものづくりの名人はたくさんの規格を知っていて、上手に活用します。規格にそって、省ける手間は極力省き、規格で対応していないような、本当に考えて作らなければならない部分に集中するのです。
プログラミングの世界にもたくさんの規格があります。基本的なものについて大まかに知っておくと良いでしょう。今回学習するのは、そんな規格の一つ、実数の仕組みの規格です。
実数をコンピュータで表現する方法はたくさんあり、それぞれに一長一短があります。使用するOSやプログラミング言語によって違います。しかし、Java言語はOSや機種によらず、これから学習する規格だけを採用しています。どのコンピュータで作ったデータも、この規格にそっているため、互いにやりとりして困ることがありません。C言語も同じ規格を使っていますので、学んで損はありません。少々の手間がかかりますが、あきらめず、課題まで取り組んでください。今回でしっかり理解してしまいましょう。
図8.1 規格を活かしててきぱき作業
実数型のしくみ
Java言語の実数[1]型は浮動小数点数という方法で表現されています。浮動小数点数とは、符号部S・指数部E・仮数部M・バイアスBとして実数Rを次のように表現する方法です。
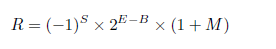
たとえば、R=－1.23であれば、
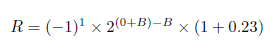
といった具合です。どうしてこんなに複雑な形にしなければならないのでしょうか。それはこのような正規化数[2]にすることで、科学技術計算に出てくる、とても大きな値やとても小さい値をコンピュータで取り扱いやすくなるからです。
プログラミング言語入門書や教科書では、「整数値は整数型に、小数を含んだ数は実数型に」という説明にとどめる場合が多いですね。実数型が浮動小数点数であることや、詳しい浮動小数点数の仕組みまで立ち入って説明されません。しかしこの知識が無いと、コンピュータで数値計算を行う場合に発生する誤差の理由が具体的にわかりません。しっかり浮動小数点数の仕組みを理解しておきましょう。
浮動小数点数は、高級[3]プログラミング言語のほとんどが対応しています。浮動小数点数にはIEEE方式やIBM方式があります。現在最も広く用いられているのはIEEE方式のIEEE754（IEEE二進化浮動小数点数演算標準）です。浮動小数点数表現は近似値表現であるため、様々な形で誤差が発生するということをよく覚えておいてください。
IEEE754とは
IEEE754とはIEEE[4]の定める浮動小数点数の表現方法の標準規格です。浮動小数点数の表現形式を規定するとともに、無限大や非数といった特殊な値も規定し、浮動小数点演算でのそれらの値の扱い方を規定しています。
単精度、倍精度など4種類[5]あり、取り扱える数値の絶対値の大きさと仮数部の桁数が異なっています。標準では単精度のみが必須とされていて、他はオプションです。
現在多くのC言語はfloatがIEEEの単精度、doubleはIEEEの倍精度[6]となっています。
Java言語はIEEE754に準拠しており、表8.1のように2つの浮動小数点数の実数型があります。
表8.1 Java言語の数値型
| バイト整数型 | byte | 8bit | -128～127 |
|---|
| 短整数型 | short | 16bit | -32768～32767 |
|---|
| 整数型 | int | 32bit | -2147483648～2147483647 |
|---|
| 長整数型 | long | 64bit | -9223372036854775808～
9223372036854775807 |
|---|
| 単精度実数型 | float | 32bit | ±1.40239846×10-45～
±3.40282347×1038 |
|---|
| 倍精度実数型 | double | 64bit | ±4.9406545841246544×10-324
～±1.79769313486231570×10308 |
|---|
IEEE754の内部
IEEE754形式の単精度は、符号部S(1ビット)・指数部E(8ビット)・仮数部M(23ビット)、倍精度は符号部S(1ビット)・指数部E(11ビット)・仮数部M(52ビット)で表現されています。各部は図8.2のように構成されています[7]。各部の意味は表8.2の通りです。
図8.2 IEEE754 のビット構成
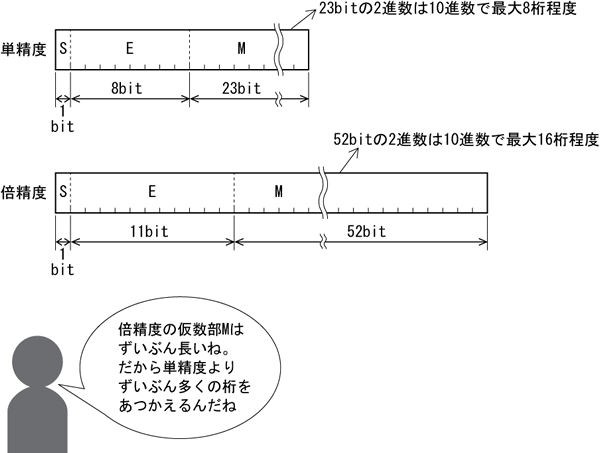
表8.2 IEEE754各ビットの意味
| 名称 | 意味 |
|---|
符号部 | 0の時は正の数、1の時は負の数を表す。 |
| 指数部 | 基数2を何乗するかを表す。 |
| 仮数部 | 仮数から1引いたもの |
指数部にはバイアス[8]がかけられています。バイアス値は単精度のとき127、倍精度なら1023です。指数部には、表8.3に示す注意すべき値があります。0を0で割ろうとするとき、また、
を求めようとすると演算結果はNaNになります。
表8.3 指数部の例外
| 指数部の値 | 左の値をとるときの意味 |
|---|
255(単精度)
2047(倍精度) | ・仮数部が0以外の時はNaN（NaN; Not a Number、非数）を表す。
・仮数部が0かつ符号部が0ならば正の無限大、符号部が1ならば負の無限大を表す。 |
| 0 | ・指数部、仮数部ともに0ならばその数は0を表す。 |
以上のことをまとめると、IEEE754形式で表現する浮動小数点数の実数Rの値は次の式で表せます。
Bはバイアス値です。前述のとおり、Rがfloat型ならB=127、double型ならB=1023です。
10進数の数値をIEEE754単精度値に変換する
10進数の数値をIEEE754単精度の規格にそった16進数表示に変換する手順を示します。倍精度の場合は仮数部、指数部の桁数とバイアス値を読みかえるだけで手順に違いはありません。単精度での変換方法をしっかり納得しておけば、倍精度で変換練習する必要はないでしょう。
表8.4にint型とfloat型の内部表現を並べて示します。たとえ負数でなくて、同じ32ビットのデータ型でも、符号付きの整数型と、単精度IEEE754の型では、中身が別物であることがよく分かるでしょう。
表8.4 型による内部表現の違い
整数型の100
単精度IEEE754の100 | (0x00000064)H
(0x42c80000)H |
|---|
IEEE754単精度値を10進数値へ変換する
IEEE754単精度値を10進数値へ変換する手順を示します。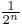
部分の計算は筆算では大変ですので、電卓を使用しましょう。
今回はここまで
次回は実数値を16進数で表示するプログラムを作ります。次に実数値を筆算と電卓で、10進数から16進数に変換してみます。
その逆に16進数で表示された実数値を、10進数に戻します。確認は自分で作成したプログラムで行います。この作業を通じて、浮動小数点数の仕組みと、長所・短所が体で理解できることでしょう。お楽しみに。
