前回までに紹介したベイズ線形回帰を実装してみます。
ベイジアンという言葉に難しい印象を持たれている方もいるかもしれませんが、
ベイジアンに難しいところがあるとすれば、
環境はこれまでと同じPython&numpy&matplotlibを使用します。インストールなどがまだの方は連載第6回を参照ください。
普通の線形回帰のコードを復習
それでは、
ガウス基底は、
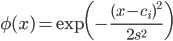
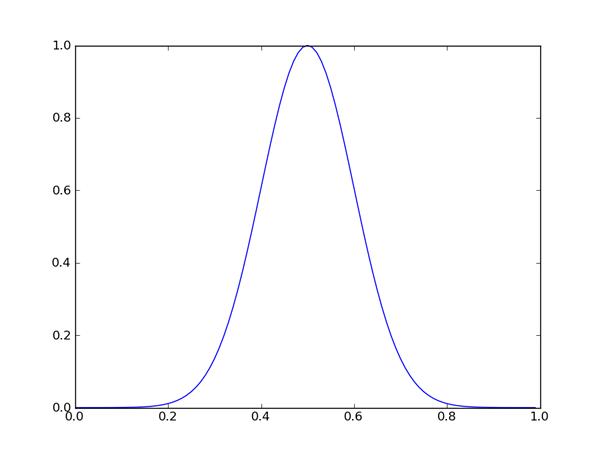
ガウス基底の良いところは、
一方の多項式基底は見慣れた多項式という形式で解を得られるというメリットの反面、
ガウス基底を使う場合、
sはデータが影響を及ぼす距離をコントロールするパラメータです。大きくするほど遠くまで影響が届くようになります。そのため小さめの値が望ましいですが、
ciはガウス基底の中心です。このガウス基底の線形和で求めたい関数を表すわけですから、
以下に第11回のコードについて、
import numpy as np
import matplotlib.pyplot as plt
X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
t = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])
# 定数項+ガウス基底(12次元)
def phi(x):
s = 0.1 # ガウス基底の「幅」
return np.append(1, np.exp(-(x - np.arange(0, 1 + s, s)) ** 2 / (2 * s * s)))
PHI = np.array([phi(x) for x in X])
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))
xlist = np.arange(0, 1, 0.01)
ylist = [np.dot(w, phi(x)) for x in xlist]
plt.plot(xlist, ylist)
plt.plot(X, t, 'o')
plt.show()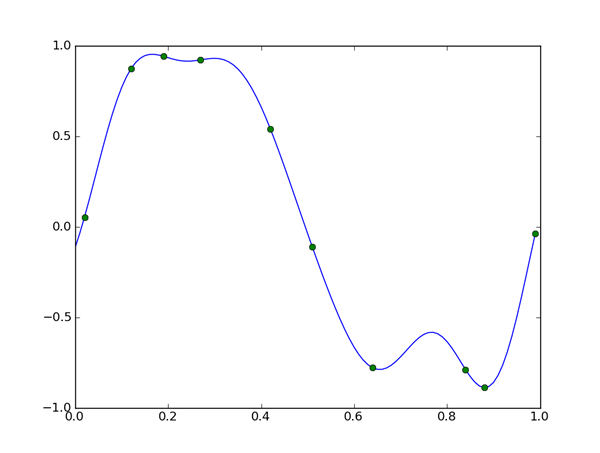
12次元のガウス基底は4次元の多項式基底よりずっと自由度と表現力が高いため、
これがベイジアンになることでどう変わるかも見て欲しいポイントです。
ちなみに今回、
その点はベイズ線形回帰も同様ですから、
事後分布の平均と共分散を求める
先ほどのコードでのxlist=~で始まる行から下はグラフを描く部分です。
ということは、
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, t))この一行をベイズ線形回帰にあわせて書き換えるのが第一ミッションです。
より具体的に言うと、
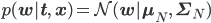
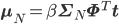
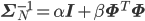
この式を実装するには、
あとは単なる行列の計算ですから、
alpha = 0.1
beta = 9.0
Sigma_N = np.linalg.inv(alpha * np.identity(PHI.shape[1]) + beta * np.dot(PHI.T, PHI))
mu_N = beta * np.dot(Sigma_N, np.dot(PHI.T, t))こうして求めたmu_
matplotlibのplot関数は続けて呼び出すことでグラフを重ねて描くことができます。色を指定するには、
xlist = np.arange(0, 1, 0.01)
plt.plot(xlist, [np.dot(w, phi(x)) for x in xlist], 'g')
plt.plot(xlist, [np.dot(mu_N, phi(x)) for x in xlist], 'b')
plt.plot(X, t, 'o')
plt.show()
具体的には、
このように、
共分散の眺め方
これで一応ベイズ線形回帰を実装して問題を解いた格好にはなりましたが、
そこでまず、
一次元の分布の
余談ですが、
しかし多次元の
# print "\n".join(' '.join("% .2f" % x for x in y) for y in Sigma_N)
2.94 -2.03 -0.92 -1.13 -1.28 -1.10 -1.21 -1.14 -1.23 -1.06 -0.96 -2.08
-2.03 2.33 -0.70 1.95 0.13 1.02 0.85 0.65 0.98 0.70 0.65 1.44
-0.92 -0.70 2.52 -1.86 1.97 -0.29 0.42 0.59 0.13 0.40 0.32 0.63
-1.13 1.95 -1.86 3.02 -1.66 1.50 0.17 0.29 0.73 0.33 0.36 0.82
-1.28 0.13 1.97 -1.66 2.82 -1.11 1.39 0.22 0.55 0.49 0.40 0.92
-1.10 1.02 -0.29 1.50 -1.11 2.39 -1.35 1.72 -0.29 0.53 0.46 0.69
-1.21 0.85 0.42 0.17 1.39 -1.35 2.94 -2.06 2.39 -0.02 0.25 1.01
-1.14 0.65 0.59 0.29 0.22 1.72 -2.06 4.05 -2.72 1.43 0.37 0.67
-1.23 0.98 0.13 0.73 0.55 -0.29 2.39 -2.72 3.96 -1.41 1.23 0.59
-1.06 0.70 0.40 0.33 0.49 0.53 -0.02 1.43 -1.41 3.30 -2.27 2.05
-0.96 0.65 0.32 0.36 0.40 0.46 0.25 0.37 1.23 -2.27 3.14 -0.86
-2.08 1.44 0.63 0.82 0.92 0.69 1.01 0.67 0.59 2.05 -0.86 2.45まずこれを見ると、
そこで
# 対角成分
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)
2.94 2.33 2.52 3.02 2.82 2.39 2.94 4.05 3.96 3.30 3.14 2.45 # 上三角行列の成分
(2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)
(1) -2.03 -0.92 -1.13 -1.28 -1.10 -1.21 -1.14 -1.23 -1.06 -0.96 -2.08
(2) -0.70 1.95 0.13 1.02 0.85 0.65 0.98 0.70 0.65 1.44
(3) -1.86 1.97 -0.29 0.42 0.59 0.13 0.40 0.32 0.63
(4) -1.66 1.50 0.17 0.29 0.73 0.33 0.36 0.82
(5) -1.11 1.39 0.22 0.55 0.49 0.40 0.92
(6) -1.35 1.72 -0.29 0.53 0.46 0.69
(7) -2.06 2.39 -0.02 0.25 1.01
(8) -2.72 1.43 0.37 0.67
(9) -1.41 1.23 0.59
(10) -2.27 2.05
(11) -0.86 これが正味の共分散行列の情報量となります。
実はこの対角成分と上三角行列をそれぞれ解釈することで、
まず対角成分ですが、
この例では一番小さいものでも2.
そして三角行列の成分は、
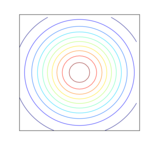
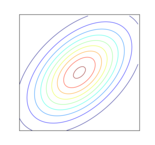
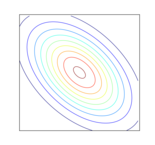
上の例をじっくり眺めてみると、
実際に問題を解くときは共分散行列をわざわざこのように眺めることはあまりしません。しかし、
予測分布を描く
共分散行列の読み方が少しわかったとはいえ、
もっと事後分布を分布として活用する方法の一つとして、
イメージ的には、
いえ、
このようにターゲットとなる変数の分布に事後分布を反映させたものを予測分布と呼びます。
今回のベイズ線形回帰の予測分布は、
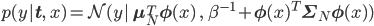
これは
matplotlibのcontourf関数を使えばそういう図を簡単に描くことができるのですが、
# 正規分布の確率密度関数
def normal_dist_pdf(x, mean, var):
return np.exp(-(x-mean) ** 2 / (2 * var)) / np.sqrt(2 * np.pi * var)
# 2次形式( x^T A x を計算)
def quad_form(A, x):
return np.dot(x, np.dot(A, x))
xlist = np.arange(0, 1, 0.01)
tlist = np.arange(-1.5, 1.5, 0.01)
z = np.array([normal_dist_pdf(tlist, np.dot(mu_N, phi(x)),
1 / beta + quad_form(Sigma_N, phi(x))) for x in xlist]).T
plt.contourf(xlist, tlist, z, 5, cmap=plt.cm.binary)
plt.plot(xlist, [np.dot(mu_N, phi(x)) for x in xlist], 'r')
plt.plot(X, t, 'go')
plt.show()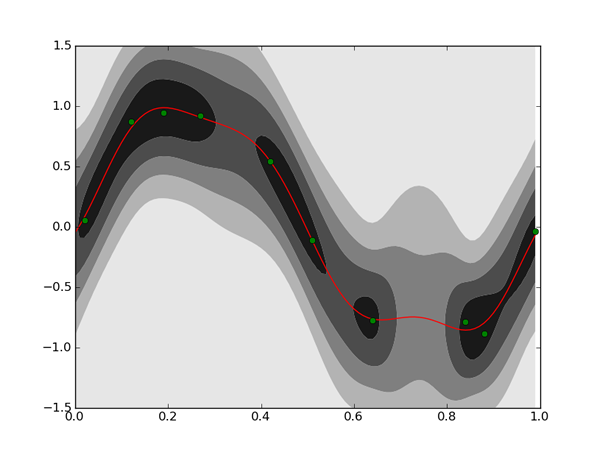
濃い部分は確率密度関数の値が高い、
こうして描いた予測分布を見ると、
普通の線形回帰では目立って
パラメータαとβの決め方
最後に、
そもそもαとβとは何だったでしょう? αは事前分布p(w)を導入するときに初めて登場しました。こういった、
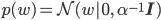
この式を見ると、
逆にαが小さいとwを押さえつける力が弱くなります。特にαが0の時は普通の線形回帰と一致します。そこで0に近い小さめの値、
もう一つのパラメータβは
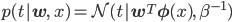
この式でβは、
つまり、
ここまでαとβを問題を解きたい人が選ぶ話をしましたが、
一番必要なのは
次回予告
次回からは分類問題の話に入っていき、



