「コロンブスの卵」的なシステムをいろいろ紹介してきたこの連載も今回が最終回になりました。コロンブスといえば「発見」ということで、最終回の今回はプログラミングと発見にまつわる話をします。
発想と発見
新しい発想を得るためには人間が時間をかけてやり方を考えたり試行錯誤したりする必要があります。前回紹介した「Scrapbox」は、少しでも関連のある情報を柔軟に思い出しやすくすることによって、発想活動を支援します。もし発想活動の一部でも計算機にやらせることができればアイデアを出す効率がアップするかもしれません。
プログラミングと発見
失敗から何かを発見したというエピソードはたくさんあります。もちろんただ失敗すれば良いというものではなく、たくさんの試行錯誤をした結果、普通と異なる挙動を見いだしたことが発見につながったということでしょう。実はプログラムを動かすことによっても、さまざまな発見ができます。こういう作業を発見的プログラミングと呼ぶことにします。
今回は、前回紹介したScrapboxの上に書いたJavaScriptコードをブラウザで実行してみたいと思います。Scrapboxにはコード記法というものがあり、プログラムなどのテキストデータをブロック表示してファイルとして外部からURLでアクセスできるので、これを使えばScrapbox上に書いたプログラムをブラウザ上で実行できます。CanvasやSVGを利用するとJavaScriptでブラウザ上に絵を描くことはできますが、初期設定などが必要で面倒なところもあるので、描画などを極端に簡単にしたP5.jsというシステムを利用することにします。
数え上げによる答えの発見
算数の問題を解くときは、理屈を使って計算するのが普通です。たとえば「鶴と亀があわせて30匹いて、足の数は全部で100本でした。鶴と亀は何匹いたでしょう?」のような「つるかめ算」を解く場合、「全部が鶴だとすると足の数は60本で、全部が亀だとすると120本になるから……」のように算数的に解くやり方もありますし、
のような1次方程式を使うこともできます。数学の問題はこのように解析的に解くのが普通ですが、図1のような総当たりプログラムを書けば、数学的知識がなくても力技で答を得ることができます。
図1 Scrapboxでつるかめ算を解く(tsurukame.js)

つるかめ算を解くのにこういうプログラムを書く人は少ないと思いますが、このような方法のほうが有利な場合もあります。もし問題が「足の数が100本以上でした」のようなものであった場合、1次方程式で普通に解くことはできませんが、上のような方法ならすべての解を網羅できてしまいます。つまり、論理的に解けなくても、簡単なプログラムを書くことによって発見的に解が得られてしまうことになります。
乱数で答えを発見
つるかめ算の場合は解の候補をすべて数え上げれば答えを発見できるはずですが、総当たりで発見が難しい場合は、乱数を使って試行錯誤的に答えを捜すこともできます。たとえば8-Queen問題を解きたいときは、再帰的に解を探索するアルゴリズムを使うのが常識的ですが、ランダムに行や列を入れ換えることを繰り返すだけでも意外と簡単に解を得ることができます。
まずこのようなデータを用意します。
* . . . . . . .
. * . . . . . .
. . * . . . . .
. . . * . . . .
. . . . * . . .
. . . . . * . .
. . . . . . * .
. . . . . . . *
2つの行をランダムに交換してみると、次のように少しだけ良い結果が得られることがあります。
* . . . . . . .
. * . . . . . .
. . . * . . . .
. . * . . . . .
. . . . * . . .
. . . . . * . .
. . . . . . * .
. . . . . . . *
これを何度も繰り返してよさげなものを残していくと、最終的に次のような答えを得ることができます。
. . * . . . . .
* . . . . . . .
. . . . . . * .
. . . . * . . .
. . . . . . . *
. * . . . . . .
. . . * . . . .
. . . . . * . .
人間は数え上げ操作が苦手ですから、8-Queenのような問題に対しては試行錯誤的に取り組んで答えを見つけることが多いですが、試行錯誤を計算機に実行させることによって、解を発見できる場合も多いでしょう。
乱数の性質の発見
乱数を使って問題を解く場合、JavaScriptのMath.random()のような「一様乱数」関数がよく利用されます。これを呼ぶと、0から1までのランダムな実数が返ります。たとえばrandom()が0.1以下の値を返す確率は1/10です。
ここまでは普通の話ですが、図2のようにrandom()で生成した座標を使って点を表示してみると図3のようになります。一様な乱数というと図4のようなイメージを連想してしまいますが、本当の乱数はこうならないことが発見できるのが面白いところです。
図2 乱数で生成した座標に点を打つ(randam.js)

図3 生成された点

図4 一様な乱数

乱数はシミュレーションやゲームでよく利用されるものですので、乱数とはどのようなものかについては、エンジニアであれば誰でもなんとなくイメージを持っていると思いますが、乱数をたくさん生成して視覚化してみるとさまざまな発見があったりします。
乱数の足し算
いくつかの乱数の平均をとると何が起こるでしょうか? ランダムなものをいくら集めてもランダムに決まっているだろうと思うかもしれませんが、実は一様な乱数をたくさん足したものは一様乱数にならず、正規分布に近づくことが中央極限定理として知られています。2つのサイコロをふった場合、その数の和が2や12になる確率よりも7になる確率のほうが大きいだろうということは直感的にわかりますが、一様乱数を足した場合も同じだということはよく考えないとわからないかもしれません。そういう場合、何も考えなくてもプログラムで実行してみればそのような性質はすぐ発見できます(図5、6)。
図5 乱数を何回か足した結果のヒストグラムを計算(normal.js)
 図6 計算結果
図6 計算結果
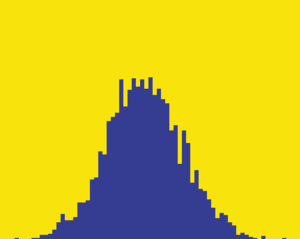
乱数の掛け算
乱数をたくさん足すと正規分布になるわけですが、では乱数をたくさん掛けるとどうなるでしょうか? 実は乱数を何度も掛け算したものは「冪分布(べきぶんぷ)」になります。図7のプログラムを実行すると図8のような冪分布になります。リニアスケールで青い点を、対数スケールで赤い点を表示しています。
図7 乱数の掛け算のプログラム例(beki.js)
 図8 実行結果
図8 実行結果
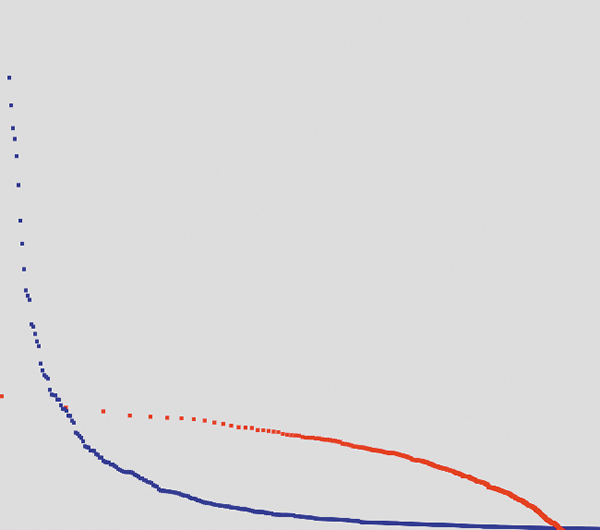
世の中には「ロングテール」と表現される冪分布がたくさんありますが、どうやらランダムな事象が掛け算的に繰り返されるとロングテール的な現象が発生するようです。
勝負の発見
まったく五分五分の勝負を繰り返した場合でも意外な片寄りを発見できます。
2人に配ったトランプの札を1枚ずつ出して勝負する「戦争ゲーム」というものがあります。このゲームは単純であまり面白いものではありませんが、そもそも勝負はつくものなのでしょうか? Scrapbox上で勝負するプログラムを図9のように書くことができます。
図9 戦争ゲームのプログラム(sensou.js)

P5.jsのdraw()がメインプロセスになって勝負の結果を表示しています。2人のプレーヤはplayer()というgeneratorで表現されており、2つのプレーヤプロセスがsetup()で初期化されています。player()もメインプロセスも無限ループになっていますが、yieldでメインプロセスと通信することにより同期しながら対戦が行われます。generator機能を利用すると、このようなシミュレータを柔軟に記述できるので便利です。
このプログラムを実行すると、意外にもすぐに決着がついてしまうことがわかります(図10)。最初の手札は同じですし、ランダムにしているにもかかわらずあっという間に総取り状態になってしまうということは感慨深いものがあります。条件がまったく同じであっても大きく勝ったり負けたりすることが発見できたことになりますが、ほんの少しのきっかけで運命が変わってしまうのは恐いものだと思います。
図10 勝負の途中

終わりに
今回紹介したプログラムはすべてScrapbox上に置いてあり、クリックするだけでブラウザ上で実行できます。Scrapboxは情報整理にたいへん便利なシステムですが、そのうえでプログラムを気軽に作成してさまざまな発見ができることでさらに広い応用が考えられると思います。
18回に渡ってコロンブスの卵的な実用的なシステムをいろいろ紹介してきました。私はこれらを毎日活用していますが、読者の皆さんもぜひ試してみていただければと思います。
- 第1特集
MySQL アプリ開発者の必修5科目
不意なトラブルに困らないためのRDB基礎知識
- 第2特集
「知りたい」「使いたい」「発信したい」をかなえる
OSSソースコードリーディングのススメ
- 特別企画
企業のシステムを支えるOSとエコシステムの全貌
[特別企画]Red Hat Enterprise Linux 9最新ガイド
- 短期連載
今さら聞けないSSH
[前編]リモートログインとコマンドの実行
- 短期連載
MySQLで学ぶ文字コード
[最終回]文字コードのハマりどころTips集
- 短期連載
新生「Ansible」徹底解説
[4]Playbookの実行環境(基礎編)














