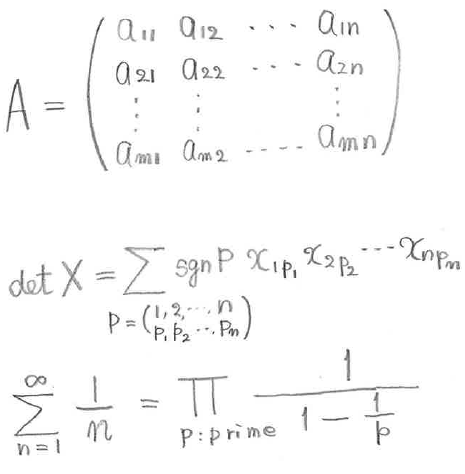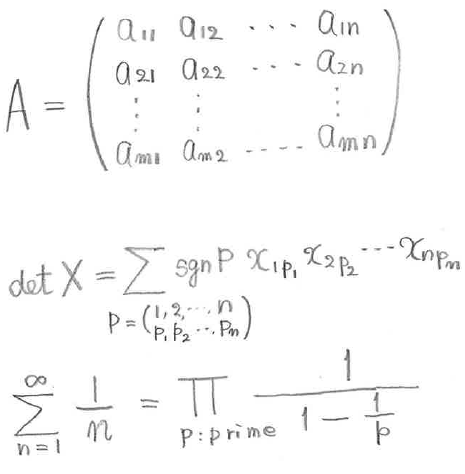しばらく前、2013年に技術評論社から『数学記号を読む辞典』という本を出版していただいた。小学校から始まる数学記号（数字、+、－など）から大学で学ぶ行列や偏微分の記号までを使用実例を挙げながら解説した本である。現在、放送大学で数学に少しだけ関係していて、何名かの学生の方から、数学記号の読み方や使い方を質問されたことがある。それも本書を執筆する動機になった。放送大学の勉強会では数学書を朗読しながら話を進めているので、文字通り物理的な読み方も問題になるのだ。実際は数学書を独習しているときは、読み方は分からなくても、記号の意味さえつかめれば大丈夫である。

数学は抽象的な学問だが、記号を使って研究を展開するという大きな特徴がある。もちろん文字も記号の一種だから、どんな学問でも記号を使って展開されるのだが、数学記号の場合、その記号列を一定の規則に従って変形できる（広い意味での計算といってもいいと思う）という特徴がある。

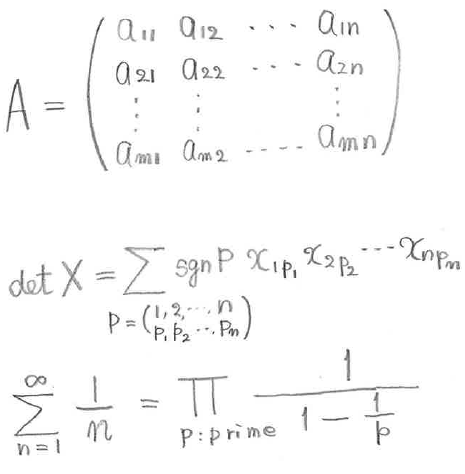
数学が数学記号を使うのは、思考過程が記号変形によって目に見える形で取り出せるからであり、その方が普通の文章表現よりずっと正確に内容を表すことができるからだ。多くの人は、記号を使うことで難しくなるのではと誤解している。そんなことはない。記号を使うことで、扱っている数学的な内容がずっと分かりやすく明確になる。数学記号は言語であり、しかも論理的に洗練された綺麗な言語なのだ。と言いつつ、線形代数学で出てくる添え字の多さに戸惑う学生さんたちを見て、なるほど、いささか面倒だなあ、と思うこともあるのですが。