前回のあらすじは、
遠近法と焦点距離
第33回
![第33回図3 [プロパティ]インスペクタの[3D位置とビュー]セクションにおける[遠近の角度] 第33回図3 [プロパティ]インスペクタの[3D位置とビュー]セクションにおける[遠近の角度]](/assets/images/dev/serial/01/as3/0033/thumb/TH800_003.png)
視野角に関わる大きさとして
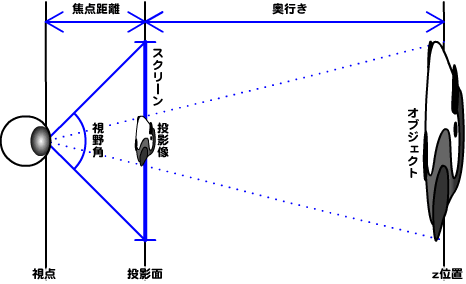
3次元空間のオブジェクトと2次元平面に投影された像との大きさの比率を求めよう。視点を頂点とし、
投影像の大きさ/オブジェクトの大きさ = 焦点距離 / (焦点距離 + z位置)投影像の大きさ = オブジェクトの大きさ×焦点距離 / (焦点距離 + z位置)この比例式は、

このように3次元空間の座標を2次元平面のxy座標に変換するとき、
焦点距離 / (焦点距離 + z位置)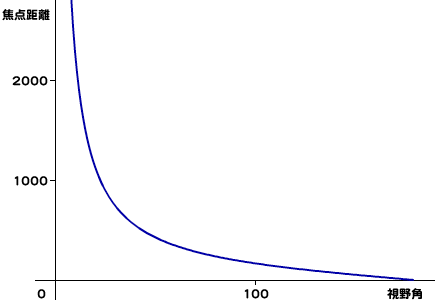
焦点距離にもとづく透視投影の計算
3次元空間座標を2次元平面に透視投影するには、
前述第33回
それでは、
function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point > {
var vertices2D:Vector.<Point> = new Vector.<Point>();
var nLength:uint = myVertices.length;
for (var i:uint = 0; i < nLength; i++) {
var myVector3D:Vector3D = myVertices[i];
// 透視投影の処理を加える
vertices2D.push(new Point(myVector3D.x, myVector3D.y));
}
return vertices2D;
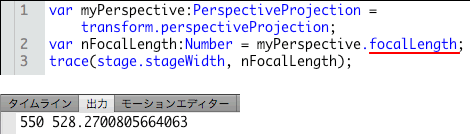
}焦点距離は、
var nFocalLength:Number = transform.perspectiveProjection.focalLength; // 追加
function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point > {
var vertices2D:Vector.<Point> = new Vector.<Point>();
var nLength:uint = myVertices.length;
for (var i:uint = 0; i < nLength; i++) {
var myVector3D:Vector3D = myVertices[i];
var nProjectionRatio:Number =
nFocalLength / (nFocalLength + myVector3D.z); // 追加
vertices2D.push(new Point(myVector3D.x * nProjectionRatio,
myVector3D.y * nProjectionRatio)); // 修正
}
return vertices2D;
}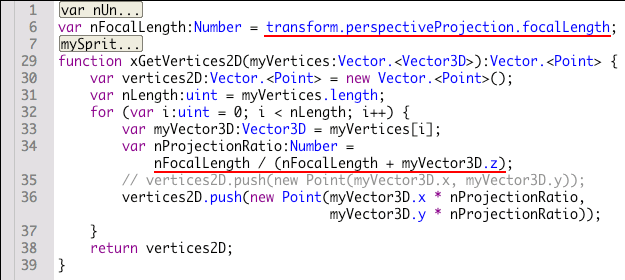
この関数の書替えで、
Vector3D.wプロパティとVector3D.project()メソッドで透視投影を行う
Vector3Dクラスには3次元座標空間における位置ベクトル
Vector3Dオブジェクト.project()このメソッドを使うときには、
第2に、
このVector3D.
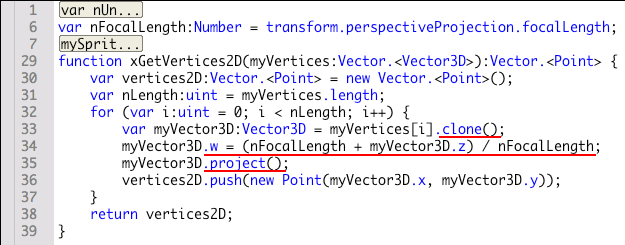
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var nFocalLength:Number = transform.perspectiveProjection.focalLength;
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
xTransform(vertices, nRotationY);
var vertices2D:Vector.<Point > = xGetVertices2D(vertices);
xDrawLines(vertices2D);
}
function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
var nLength:uint = myVertices.length;
var myMatrix3D:Matrix3D = new Matrix3D();
myMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
for (var i:int = 0; i<nLength; i++) {
myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
}
}
function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point > {
var vertices2D:Vector.<Point> = new Vector.<Point>();
var nLength:uint = myVertices.length;
for (var i:uint = 0; i < nLength; i++) {
var myVector3D:Vector3D = myVertices[i].clone();
// Vector3D.wプロパティ = (焦点距離 + z位置) / 焦点距離
myVector3D.w = (nFocalLength + myVector3D.z) / nFocalLength;
myVector3D.project();
vertices2D.push(new Point(myVector3D.x, myVector3D.y));
}
return vertices2D;
}
function xDrawLines(vertices2D:Vector.<Point>):void {
var nLength:uint = vertices2D.length;
var myPoint:Point = vertices2D[nLength - 1];
myGraphics.clear();
myGraphics.lineStyle(2, 0x0000FF);
myGraphics.moveTo(myPoint.x, myPoint.y);
for (var i:uint = 0; i < nLength; i++) {
myPoint = vertices2D[i];
myGraphics.lineTo(myPoint.x, myPoint.y);
}
}[ムービープレビュー]
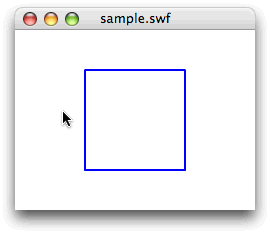
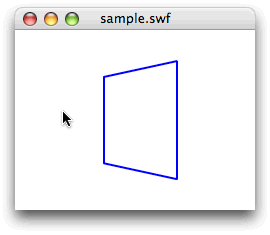
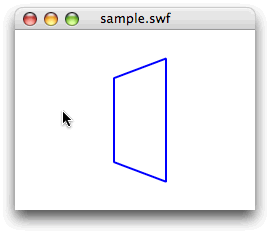
今回解説した次のサンプルファイルがダウンロードできます。
- スクリプト1のサンプルファイル
(CS4形式/ 約19KB)



