はじめに
前回は、
凸多角形による疑似半平面表現
前回も述べた通り、
図1を見てください。点線で囲まれた正方形の内部が、
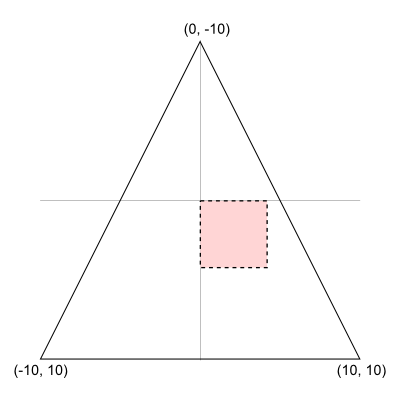
ある直線が与えられたとき、
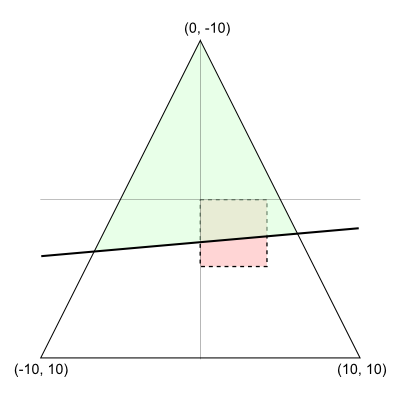
実際にこの切断を行い、
execute()メソッドは、
public class PseudoHalfPlaneGenerator {
private Point2D boundary1; // 境界点1
private Point2D boundary2; // 境界点2
private Point2D boundary3; // 境界点3
private LineSegment border1; // 境界線1
private LineSegment border2; // 境界線2
private LineSegment border3; // 境界線3
private double distanceThreshold; // 交差の場合分けを正確に行うための閾値
// boundaryの値を大きくすると計算誤差が無視できなくなるので注意!
public PseudoHalfPlaneGenerator(double boundary) {
boundary1 = new Point2D.Double(0, -boundary);
boundary2 = new Point2D.Double(-boundary, boundary);
boundary3 = new Point2D.Double(boundary, boundary);
border1 = new LineSegment(boundary1, boundary2);
border2 = new LineSegment(boundary2, boundary3);
border3 = new LineSegment(boundary3, boundary1);
distanceThreshold = boundary / 1000.0;
}
public ConvexPolygon execute(Line line, Point2D example) {
// lineと各境界線の交差を調べる
Point2D p1 = border1.getIntersectionPoint(line);
Point2D p2 = border2.getIntersectionPoint(line);
Point2D p3 = border3.getIntersectionPoint(line);
List<Point2D> vertices = new ArrayList<Point2D>();
// lineが境界線1および2と交差する場合
if (p1 != null && p2 != null && p1.distance(p2) >= distanceThreshold) {
// 境界点2とexampleがlineから見て同じ側にあるなら
if (GeomUtils.ccw(p1, boundary2, p2)
* GeomUtils.ccw(p1, example, p2) > 0) {
// 境界点2を含む方の切断後頂点リストを生成
addVertices(vertices, p1, boundary2, p2);
} else { // そうでないなら
// 境界点2を含まない方の切断後頂点リストを生成
addVertices(vertices, p1, p2, boundary3, boundary1);
}
} else if (p2 != null && p3 != null
&& p2.distance(p3) >= distanceThreshold) { // lineが境界線2および3と交差する場合
// 境界点3とexampleがlineから見て同じ側にあるなら
if (GeomUtils.ccw(p2, boundary3, p3)
* GeomUtils.ccw(p2, example, p3) > 0) {
// 境界点3を含む方の切断後頂点リストを生成
addVertices(vertices, p2, boundary3, p3);
} else { // そうでないなら
// 境界点3を含まない方の切断後頂点リストを生成
addVertices(vertices, p2, p3, boundary1, boundary2);
}
} else if (p3 != null && p1 != null
&& p3.distance(p1) >= distanceThreshold) { // lineが境界線3および1と交差する場合
// 境界点1とexampleがlineから見て同じ側にあるなら
if (GeomUtils.ccw(p3, boundary1, p1)
* GeomUtils.ccw(p3, example, p1) > 0) {
// 境界点1を含む方の切断後頂点リストを生成
addVertices(vertices, p3, boundary1, p1);
} else { // そうでないなら
// 境界点1を含まない方の切断後頂点リストを生成
addVertices(vertices, p3, p1, boundary2, boundary3);
}
} else {
throw new IllegalArgumentException(
"Cannot create a pseudo half plane.");
}
// 頂点リストから凸多角形を生成して返す
return new ConvexPolygon(vertices);
}
// listにpointsを追加する。このとき、同一座標の重複追加を避ける
private void addVertices(List<Point2D> list, Point2D... points) {
for (Point2D p : points) {
if (list.isEmpty()) {
list.add(p);
} else {
Point2D first = list.get(0);
Point2D last = list.get(list.size() - 1);
if (!p.equals(first) && !p.equals(last)) {
list.add(p);
}
}
}
}
}ボロノイ領域の計算
それではいよいよ、
ある母点のボロノイ領域を求める方針は、
以上の方針にしたがって、
public class VoronoiGenerator {
private PseudoHalfPlaneGenerator halfPlaneGenerator = new PseudoHalfPlaneGenerator(
10); // この値を大きくしすぎると計算誤差が無視できなくなる
private PolygonIntersectionCalculator intersectionCalculator = new PolygonIntersectionCalculator();
// areaの領域内で、母点sitesの各ボロノイ領域をリストにして返す。
// areaおよびsitesの各座標が、halfPlaneGeneratorの境界内に収まるように注意すること
public List<ConvexPolygon> execute(ConvexPolygon area, List<Point2D> sites) {
List<ConvexPolygon> result = new ArrayList<ConvexPolygon>();
for (Point2D s1 : sites) {
ConvexPolygon region = null; // 途中計算結果格納用の領域
for (Point2D s2 : sites) {
if (s1 == s2) {
continue;
}
// s1とs2の垂直二等分線を求める
Line line = Line.perpendicularBisector(s1, s2);
// 垂直二等分線による半平面のうち、s1を含む方を求める
ConvexPolygon halfPlane = halfPlaneGenerator.execute(line, s1);
if (region == null) { // 初回計算時なら
// areaと半平面の交差を求める
region = intersectionCalculator.execute(area, halfPlane);
} else { // 2回目以降なら
// これまでの計算結果と半平面の交差を求める
region = intersectionCalculator.execute(region, halfPlane);
}
}
// 最終的な計算結果をボロノイ領域とする
result.add(region);
}
return result;
}
}VoronoiGeneratorクラスのexecute()メソッドは、
デモプログラム
今回解説したアルゴリズムをグラフィカルに動作確認できるよう、
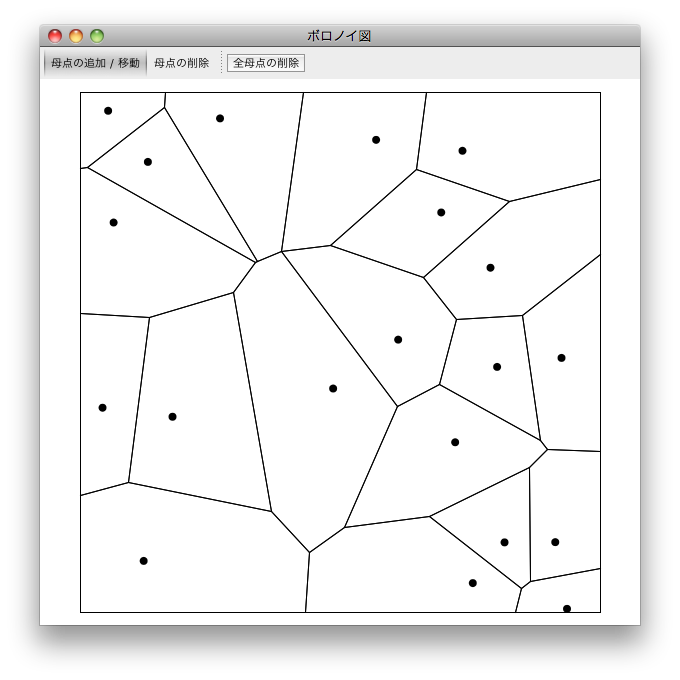
デモプログラムを起動すると、
最後に
最終回となる今回は、
今回作成したプログラムのソースコードは、
本連載をきっかけとして、



