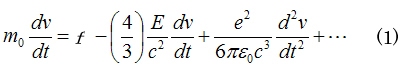前回 は1923年に新しい時代が動き始めたこと、そして湯川に象徴される日本の時代を書きました。
今回は趣を変えて、ライバル関係にある2人の物理学者の対話という場面で、2つの時代を見てみようと思います。
一つの場面は(前半)1909年のザルツブルグで、もう一つ(後半)は1933年の仙台です。
前半は、いままでどおりの「ですます調」で語りますが、後半はまた趣を変えて「である調」にしてみました。
1.アインシュタインとハーゼンエール(ザルツブルグの学会で)
『ピタゴラスの定理でわかる相対性理論』とこの補講で、ハーゼンエール(Friedrich Hasenöhrl)のことを書いてきました。詳細は以下を参照してください。
今回新たに、アインシュタインとハーゼンエールが、会って話をしていることがわかりました。それは1909年9月21日にザルツブルグで開かれた学会、「 第81回ドイツ自然科学者と医学者の会合(Gesellschaft Deutscher Naturfolscher und Ärtze in Salzburg) 」のあるセッションです。
司会をしたのはマックス・プランクでした。このときの記録が、同年11月10日のPhysikalische Zeitschrift 10 に掲載されているのです。これはE=mc2 に関連する議論です。
これを紹介するまえに、アインシュタインが考えていたことについて、若干の私見を語っておきたいと思います。
E=mc2 論文の見城の訳の意義について一言アインシュタインの業績について興味を持つ読者にとって『アインシュタイン選集』[ ※1 ]は貴重な資料だと思います。しかし一つだけ苦言を申し上げたいのです。ここにはアインシュタインの主要論文の翻訳が入っています。
第12回にとりあげた ( 光電効果に関する)1905年 3月論文は、細かな見解の相違を別にすれば正確な良い訳だと思いますが、( 質量とエネルギーに関する)9月論文は、誤訳というか手抜きだと思います。
まずドイツ語の原文からではなく、ロンドンで出た英語版からの訳であることに失望します。その英語版には原文を意訳した部分があり、湯川版にはそれをまた誤訳したところがあります。それは許すとしても、記号に決定的なエラーがあります。
アインシュタインは、光速を大文字のV で表しています。英語版は現代風に小文字のc に変えています。アインシュタイン選集の訳では、もともと大文字のC で表していた定数まで小文字にしたために、V とC の区別がなくなって両方ともc になっています。しかもそのあたりこそアインシュタインの頭脳がドイツ語で考えて表現したエッセンスなのに、英訳版を(輪講での大学院生のように)辞書からもってきた訳語で埋めあわせた日本語の羅列のために意味が通じません。調べてみますと版を重ねても直っていません。このあたり、ひょっとすると湯川も理解していなかったのではないかという疑念さえ生まれます。
さて誤訳というのは、E=mc2 の意味を述べた部分です。
原文:
(これの見城訳 )ここで物体から引き出されるエネルギーが輻射のエネルギー(訳者注:光の放射)に変換されることは明らかに本質ではないので、次の一般的な推論に到達する。
(推論部分は訳のみ)物体の質量はそのエネルギー量(中身)の一つの尺度である。エネルギーがL エルグだけ変化(増減)すると、その質量はL/9×1020 グラムだけ変化(増減)することを意味する。
これのロンドン英訳は以下のようになっています。
The fact that the energy withdrawn from the body becomes the energy of radiation evidently makes no difference, so that we are led to the more general conclusion that(推論部) .
少し解説します。the fact(事実)という語が英訳に現れるのですが、ドイツ語の原文にはありません。
この英語を訳すと次のようになります。
物体から引き出されるエネルギーが輻射のエネルギーになるという事実は明らかに本質的なことではないので、次のより一般的な結論に到達する:
(推論部分の英訳には問題がないのでその日本語訳は上とほぼ同じ内容)
さてここで注意したいのは、to make no differenceは「重要ではない」という意味です。
しかしアインシュタイン選集では、物体から引き出されるエネルギーが、輻射のエネルギーになることは事実であるから、( 推論部) 。
となっています。
おそらく、英語からの訳者はevidently makes no differenceを「明らかに違いない」事実、と解釈したのだと思います。英語の意味としては平易にいうと「明らかにどうでもよいこと」という意味です。
ちなみに、この補講の第10回目 は、この論文の原文を見ながら翻訳して論じたものです。筆者が『アインシュタイン選集』の翻訳を見たのはこの後でした。あらためて自分の訳をみたところ、自分にも若干の不注意があったのでこのたび修正しました。このあたりの筆者の解釈ですが、原文では「エネルギーが(別段輻射ではなくても)L エルグだけ変化すると、その質量はL /9×1020 グラムだけ変化(増減)することを意味します」と言いたかったのだろうと思います。
つまり、輻射以外のエネルギーも想定内だと思います。一方、アインシュタイン選集の訳では、質量が減るとそれはかならず輻射のエネルギーになるのだと断定してしまいます。このように、重訳には微妙なところで原文とは違う意味になる危険が付きまとうものです。
アインシュタインとハーゼンエールの会話(輻射の変動)
さて、当時のドイツ語圏の学会の雰囲気が若干感じられる資料[※2 ]が見つかったわけです。場所はザルツブルグでした。この学会で、ハーゼンエールは理論計算によって、閉じ込められた空間の中のガス分子がもっている運動エネルギーが、徐々に輻射のエネルギーに変化していくという結果を示しました。実際にはそれよりも速く変化します。この資料によると、アインシュタインはこの問題について自分の考えを同じセッションでハーゼンエールよりも先に発表したようです。
講演後に印刷された論文でハーゼンエールは「アインシュタインの仮説によると、ここで問題としている効果は輻射の不規則性によって打ち消されてしまう。」と述べています。質疑応答の議事録として、ここには次の会話が記録されています。
アインシュタイン: 「確かにこの場合にはまさに不規則な変動(揺れ)ですからマックスウェルの分布則が成り立ちます。つまり減衰は不規則な衝突によって補償(うち消)されます。」 ハーゼンエール: 「貴殿の説をよく理解できているかどうかわかりませんが、もし閉じた容器の中のことを考えて、物体はその中でのみ動きまわるとします。すると輻射による(運動エネルギーの)減衰はないとお考えでしょうか? アインシュタイン: 「Jawohl(ヤボール、おっしゃるとおりです。) 」 ハーゼンエール: 「私の考えでは、最初は動きの減衰は顕著ですが、次第に長い時間をかけて減衰します。」 プランク: 「お二人がよって立つ前提が違っているのではないでしょうか。ハーゼンエール先生は完全に一様な輻射の強さを考察しています。一方、アインシュタイン先生は輻射の変動を考察して、さらにその結果として起きる作用の変動を考えると全体としての減衰にはならないとしています。」
(注) (統)御することができない(こと)という意味で、無秩序という訳があてられることもある。つまり、気体分子の動きのようなもので、分子の速度や方向にバイアスをかける状態がないこと。プラズマ状態のように電離しているときに外部から磁界や電界をかけると、電子やイオンの動きに一定の作用をするので無秩序とはいえなくなる。そのようなバイアスがないときの統計的な状態が、マックスウェルの分布として知られる状態。Unregelmäβigにあたる英語はirregularだが、日常的には不規則なよりも異常なというニュアンスを感じるので要注意。
これは、E=mc2 あるいはE=(3/4)mc2 が背景にある議論です。二人が異なる理論的考察によって類似の関係を得たものです。ハーゼンエールの考察は黒体のなかの輻射エネルギーの変化の仕方に関するものです。
このあたりの議論を現代の知識をもって読むのか、私どもをその時代と場所に投げだして考えるかによって価値が違うかもしれません。ニュートン力学の運動エネルギーは0.5mv2 に帰結するのですが、輻射とは光のエネルギーですから、アインシュタインの光量子にまで関係する複雑な問題です。
E=amc2 ( ただしaは1あるいはそれに近い係数) に関して、1905年前後の研究者は、輻射に伴う慣性質量(inertial mass)という発想で考察されてきました。ハーゼンエールが1904年の論文で導いたのは次のような結論です。
閉じた容器が輻射で満たされていて、その容器が速度v で運動しているとき、輻射のエネルギーは若干大きくなるのだが、運動エネルギーに換算したときの質量の見かけ上の増加は速度に無関係に
である。
ただし、第2回 でも記したように、Max Abrahamの指摘によって係数に計算違いがあって正しくは
です。
ここで重要なことが、ハーゼンエールは質量が⊿ m だけ減るときに発生するエネルギーE がE=(3/4)mc2 であるとは言っていないことです。
この論文が書かれた1904年には、アインシュタインの光量子説は出ていません。ではこの1909年にハーゼンエールは、それを認めていたかどうか筆者にはわかりません(どなたかハーゼンエールの1910年の論文を調べていただけるでしょうか?) 。
ザルツブルグでの3人の討論(アインシュタイン、ハーゼンエール、プランク)ですが、当時はテープレコーダがありませんでしたから、この応答の記録があったとすれば速記だったでしょう。会話の応答を簡潔な文書にするときには、正確になるのかどうか疑問です。
司会のプランクがかなりの見識をもってまとめたのか、あるいは彼もまあまあこのあたりで両者を立てて議論を終わりにしたとも考えられます。
もう一つ補足すると、ハーゼンエールは「放射と量子」をテーマとした1911年に開かれた最初のソルベー会議と13年の第2回会議に招待されています。この議事録を見れば、この3人がE=mc2 の問題についてふたたびどんな議論をしたかはある程度わかるはずです。
Wikipediaで「Solvay Conference」を検索して出てくる写真 ハーゼンエールです。彼は第1次世界大戦で志願して1915年に戦死したことは第2回にも書いたとおりです。ハーゼンエールの最初の学生だったシュレディンガーが、ソルベー会議に招待されたのは1927年の第5回です。
ここで繰り返して重要なことは、ハーゼンエールが、輻射エネルギーは等価の質量を持つことを古典論のプロセスで導いていたことです。ですから、E=amc2 の関係が相対性理論特有のものというのでなかったのです。
ところが、相対性理論によってアインシュタインが手品のように手短かな論理によって導いたことは、新しいパラダイムの誕生だったといえます。ハーゼンエールが導いたように閉じた空間での複雑な論理ではなく、アインシュタインが前提としたのは、対象は剛体、時計の概念(時間の相対性) 、光の速度が観測者の速度には依存しない、という3つでした。
その結果、係数a は3/4ではなく1でした。しかし、第10回 にも述べたように、アインシュタインは数式(方程式)の形ではなく、文章で表したことに意味があると思います。そしてアインシュタインはこの意味をさらに深く考えようとしたのではあるまいか、そう思えてなりません。彼は質量の減少は、必ず放射(輻射)になるとは言い切ろうとはしてなかったと思います。
当時のイギリスではどうだったか
Edmund Whittaker のAether and Electricityによると,電子の発見で有名がJ.J.トムソンが1881年に荷電した球状導体が直線運動するとき、電界のエネルギーをE とすると、質量が (4/3) E/c2 ハーゼンエールが黒体輻射について計算した上の結論と一致します。
これも重要なことですが、エーテルの仮説があった1900年当時、フランスのポアンカレは、ポインティングのエネルギー流がそれに(1/c2 ) 電磁エネルギーは(1/c2 )
1909年といえば、アインシュタインはベルンの特許局に辞表を出してチューリッヒ大学に移っています。
イギリスでは、マックスウェルの伝統を引き継ぐケンブリッジ大学が、理論物理のメッカでした。当時のケンブリッジではLarmorという先生が、アインシタインの向こうを張っていました。よく言われるように質量には、重力に関係して定義される質量と、慣性に関連した質量があって、それを統一的に解決したのがアインシュタインの一般相対性理論です。この理論ができる以前からLarmorは特殊相対性理論を認めませんでした。物質の質量は、物質のもつ電荷によって説明できるのだという信念の持ち主でした。電荷は電界エネルギーを伴うので、質量と電磁界のエネルギーは互いに関係があると考える思想です。この考えでは、やはりハーゼンエールの関係式のようなものが出てきます。
これが半分当たりで、半分エラーだったのですが、当たりの方をつぎの砂川の理論で見てみましょう。
1907年ごろからケンブリッジ大学の若手の中に、たびたびドイツに行ってドイツ語で物理を学ぶ者が出てきて、アインシュタインともコンタクトをとるようになります。1919年に一般相対性理論の正しいことを確認したのが、ケンブリッジ天文台長のエディントンであり、この反省を契機にケンブリッジ大学は、ディラックのような気鋭を育成するようになります。このあたりのことを詳しく書いているのがAndrew WarwickのMaster of Theory [ ※3 ]です。
砂川重信の『理論電磁気学』[※4 ]のすばらしさ
有り難いことに、慣性質量について単純なモデルを使って日本語で詳細に考察していたのが砂川重信です。砂川は、場の量子論の専門家で大阪・東北の両大学で教授をしていました。砂川は、電子の運動方程式を非相対論で追究すると、次式になることを説明しています。
ただし
m0 = 電子の裸質量v = 電子の速度f = 他の電子の影響によって受ける力ε0 = 真空の誘電率
(1)式右辺の第2項は自己力というもので、自分の作る電磁界によって受ける力です。右辺第3項以降は、数学の手順として級数展開したときに現れるもので、光速cが大きいので近似的に無視できます。
電磁気を考えないニュートン力学では
ですから、これに合わせるように(1)式を書き換えると次のようになります。
これはJ.J.トムソンの結論と一致するのですが、砂川の論理は、運動が直線と限らない一般の場合で成り立つことを説明しています。
このように電子は、本来の自分自身の質量m0 に加えて⊿m が付加されています。⊿m は自分自身の電荷のために現れる見かけ上の質量の増加で、電磁的質量(あるいは着物質量)と呼ばれるもので、ハーゼンエールが得たと同じ形になります。
このように異なる場面で、同じ式が現れることに意義があると思います。輻射は電磁界のエネルギーですから、まさにこれは電子の運動エネルギーと輻射エネルギーの相互の関係です。
(5)式に係数(4/3)が現れるために、相対性理論の結果と異なる原因について砂川はさまざまに論じているのですが、一つは、電子が有限の半径aをもつ剛体としていることが相対性理論と相容れない一つの要因だとしています。つまり、半径a→0とすればそれは解決するのですが、( 2)式のエネルギーは∞になり電磁的な質量も∞になってします。このあたりの暫定的な解決として、後に述べる朝永振一郎の繰り込み理論が出てきたのだと思います。
電子が他の電子の影響を受けながら運動するとき、通常の力学とは違って自分が作る電磁界の影響も受けるので、見掛けの質量が大きくなる。
政治的意味をもった係数1
前回にも書いたことですが、 E=mc2 が政治的・軍事的な意味をもつようになったのは、ドイツのハーンとシュトラスマンによるウラニウムの核分裂現象の発見(1938年)によるものでした。アインシュタインとハーゼンエールの議論からほぼ20年の後です。
ハーゼンエールは第1次大戦でイタリア軍の手榴弾で戦死しますから、この式が重大な意味をもつことを知らなかったはずです。当人同士は、学会の懇親会などではどんな話をしたのでしょうか? そんな資料があればと期待しています。
アインシュタインの式とされるE=mc2 があまりにも簡潔なこともあって、またマンハッタン計画という大プロジェクトがあって、アインシュタインと原爆とが結びつけられたことは、彼にとっては生涯の不本意だと思います。核分裂による質量の減少が、強力な輻射エネルギーになることをそのまま利用したのが原爆です。現在では原子力発電のエネルギー源です。アインシュタインは、この式にもっと別の期待をしていたように思えてなりません。
2.湯川と朝永(東北大学のグランドで場と素粒子を論じる)
ドキュメンタリー作家松尾博志は、湯川と朝永の生涯の交錯を徹底的にたどろうとした。その仕事をしていくと、そこに八木秀次という「書き手の心をひきつける科学者」が浮上してきたという。そして『電子立国日本を育てた男』( 文藝春秋)として結実した。タイトルに若干の不自然さを感じるのだが、それには訳がある。八木という人物は人の才能を多方面で人を開花させたからだ。
その例を年代順に3つ挙げよう。八木は、1914年から翌年まで無線技術のためにロンドンでの留学中に大英博物館の東洋学者アーサー・ウェーレーの日本語(といっても古典)と漢文読解の手助けをする。その結果、ウェーレーはやがて源氏物語を英訳し(The Tale of Genji)一躍有名になった。
もう一つは仙台の東北大学で指向性アンテナを発明して、日本の電子工学を担う人材を育成した。このことを疑う人はいないだろう。
そして、日本の物理学を1930年代に世界レベルに引き上げる環境と人材を、大阪大学に築いたことだ。
この本の第7章(湯川秀樹と朝永振一郎、P.199)に、京都大学にいた湯川秀樹が仙台で八木に始めて会ったときのことと、多分その翌日の昼休に東北大学のキャンパスグランドで朝永振一郎と新しい粒子の予言について、小枝で数式を書きながら論じた場面が克明に書かれている。この場面が何とも不思議である。
歴史を遡る。1922年にアインシュタインは、来日したときのことを後年になって思い返して、本多光太郎、日下部四太郎、愛知恵一、石原純がいた当時の東北大学は物理学の脅威だといった。このなかで日本の鉄鋼・金属産業の発展に大きな足跡を残したのが本多であり、八木との交友も深かった。
八木がドイツ(ドレスデン) 、イギリス(ロンドン) 、アメリカ(ハーバード)での3年半にもおよぶ研修を終えて仙台に戻ったのは1916年だが、3年後の1919年に東北大学に工学部ができて、彼は電気工学科を創設した。
イノベーションの実績は物理学科から電気工学に移っていった。国力を左右する技術が波長の短い強力な電波の発振と受信技術である。1920年には八木が留学していたドレスデン工科大学では大きな進歩があって、東北大を日本の弱電技術の中心にしようとしていた八木の士気を高めていたに違いない。
1923年に、学生が実験中に不思議な現象を見つけたのがきっかけで、1925年にはいわゆる八木アンテナの原理が確立され、宇田の詳細な実用化研究によって八木・宇田アンテナが発展した。
1927年には、岡部金次郎が陽極分割型マグネトロンを発明して強力な超短波を発信する真空管ができる。東北大学に発明・発見の雰囲気がみなぎっていたのだ。それは八木秀次という異才によるものだと筆者は思う。
ところが、1931年に大阪帝国大学の設立があって、学長を引きうけた長岡半太郎は八木に物理学科の創設を頼んだ。しばらくは600kmも遠方の東北帝大との兼務である。彼は理論物理の若手として朝永と湯川を候補リストに挙げていた。しかし朝永は、すでに仁科が理研に獲得していた。1933年の四月、東北大学で数学物理学会の年次学会があり、物理関係者は仙台に集まっていた。
湯川は、八木を市内に借りていた応接室に訪ねて、窮屈な京都大学から新設の大阪に移りたいと願った。八木は即決した。おそらく、内気そうで静かな声の内面にある大望を湯川に感じ取ったのだろう。
その翌日の昼休みだろう。湯川はクラスメートだった朝永と大学のグランドを散歩し、立ち止まって小枝で地面に数式を書きながら、けったいな粒子のことを話題にして朝永の考えを聞こうとしたのだ。この問題で対等に議論できる相手は、日本には朝永しかいなかったのだ。
このディスカッションを辿ってみて凄いと思うのは、クラスメートであると同時に、ともにノーベル物理学賞をとることになるライバル同士の心理描写である。
松尾はこのあたりについて膨大な資料を集めて考えた。核力を解明するための量子力学についての鋭さにおいて、通常の文科作家とは違う松尾は、この2人がこのときに思ったことはこれしかないと確信して書いたという。
朝永は誰からも優秀で快活と認められていた。余裕を感じさせていたに違いない。湯川は第三高等学校の時代から、ドイツから来る物理の雑誌をねずみが餌をかじるように読んでいた。京都大学の講師時代といっても、日本に物理学の先端を教える大学があることすら欧米には知られていなかったときに、真剣に原子核の中の内部の陽子と中性子を結びつける強力な力を正攻法で理論づけようとしていたのだ。
核内にシュレディンガーの波動方程式が適用できるかどうか疑問視されていたときに、波動方程式を持ち込み、電子が核力に関与しているだろうというハイゼンベルグの仮説を堂々と批判した。
このとき東北大のグランドで湯川は、よもや朝永が理研で類似の問題で、先を行っているのではあるまいかと詮索していた。しかし朝永は、「 けったいな粒子」の存在を湯川から聞いて、たじろぎ始めたのだ。兎が亀に追い越され始めたことを感じたのかもしれない。翌日、湯川は「核内電子に関する一考察」と題して発表した。そのときの仁科芳雄の質問の様子は資料にも残っていて、松尾はそれにもとづいた記述をしている。読者にはこの書を手にとって読んでいただきたい。
ちなみに湯川はこのときの発表を論文にはしなかった。松尾が言うように、突っ込みを怠ってしまったのか、あるいは、湯川は納得のいかない中途半端な論文を書きたくなかったのだろうか? その前年の1932年に陽子とほとんど同じ質量を有し電荷をもたない粒子の証明がイギリスのジェームス・チャドウィックの一連の実験によってなされた。これが中性子である。そこで問題になっていたのが、原子核内の複数の陽子同士を結びつける強力な引力(これを核力という)とβ 崩壊という現象だった。β 崩壊とは中性子がβ線(電子)とニュートリーノの組を発生して陽子に変化する現象である。β線が発生するので、核力を担う粒子として電子が核内にあるだろうという予測があった。このとき、湯川も朝永もニュートリーノをまだ知らなかった。ヨーロッパではオーストリアのパウリがその存在を語っていたが自信がなく論文にはしていなかったので、物理の辺境の地日本には聞こえてこなかった。
ここで「粒子と場」について筆者のコメントを加えよう。電子は物質の最小単位の一つで粒子である。光にも最小単位の光子がある。光は電磁波でもあるが、電磁波と並存する光子が最小単位であれば電磁界(電磁場)にも最小単位がある。つまり場の量子である。ということは場と量子は対の関係をもつ。核内の局所に働く力の場の対になる量子が電子だろうという発想があったし、湯川もそう考えた。ところがシュレディンガーの波動方程式を立てて解析すると核力の到達距離が実際よりもかなり大きくなってしまうのが、湯川の問題だったのだろう。もう一つ、スピンが合わないことも問題だった。
逆に、核力の場の範囲を実験からわかっている数値にすると、質量のかなり大きな粒子(量子)が存在することになり、「 そんなものあらへんで」ということになったのだ。
八木と湯川
1933年5月に、湯川は阪大に移って講義を始めた。論理明晰だったが、迫力なく学生には眠気を催すしゃべり方だったらしい。それから1年になろうとするある日の夕方、湯川は八木の部屋で痛烈な面責を受けた。湯川は大学卒業後5年になるが論文がなかった。そのことは本書のp.30~36に「湯川秀樹の鬱屈」という見出しで書かれている。部分を引用しよう。
「君が去年の春に仙台の学会で発表した核内電子の研究を聞いて、私はなかなか面白いと思ったよ。量子力学の一番先っちょに取り付いて、ほかのだれもがやっていないようなことを考えていると思った。私は君のそこを買ったんだよ。…………あの発表は結局論文にはしなったらしいが、それはいいとしても、その後もいっこうに論文がでてこないではないか。…………」 八木は、この苦言では本当は君ではなくて朝永君を採りたかったということまで言って、湯川の自尊心を十分に傷つけている。いや、普通なら傷つけられるし、そのために出勤もできない心理状態になっても現代では不思議ではない。
(ここは『電子立国日本を育てた男』第8章P.251になるが)八木が同年6月に半年の海外出張に立つ前に、湯川は今度は伏見康治を引き合いに出されて論文を促された。湯川は八木が帰国するまでに核力の問題を解決したかった。伏見が見つけたフェルミのイタリア語論文でニュートリーノを知ってヒントが得られて、八木の帰国とほぼ同時に計算ができ上がって、セミナー発表、論文執筆となったことは前回に書いた。これも松尾の著作をもとにした記述である。
湯川の1935年の論文[※5 ]はproton(陽子)とneutron(中性子) という用語で論じているが、定冠詞の使い方が正統な英語とは違っているのかドイツ語の影響を受けているのか、1個のprotonと1個のneutronの関係を厳密に論じているのか、文体だけでは判然としないところがある。彼の英語にケチをつけようというのではなく、陽子のほかに中性子の存在がほぼ実験で確認された直後にこれらの粒子の間の核力を、日本語を母語として漢籍にも明るく、ドイツ語と英語が使える頭脳で導きだしたことが重要である。それを英語で論じたのだ。( 湯川は大戦中は対戦国の英語を使わず、同盟国のドイツ語で論文を書いた。)
この英語論文では、ハイゼンベルグのいうPlatzwechselという用語はドイツ語のままになっている。これは英語に直訳すればplace exchange あるいはposition exchangeであり、陽子と中性子が核力粒子(中間子)をキャッチボールするとき、互いの位置を交換することである。しかし独・英の技術用語辞典を調べると、最初にphantom transportationとあって幻想輸送というふうな神秘的な意味をもつ用語かもしれない。
この論文の脚注に、陽子と中性子の作用に関する計算にはハイゼンベルグの理論を使ったが、朝永に負うところが大きかったと記している。
松尾によると、欧米の物理学者が回想して、「 新粒子の発見の驚きよりも、それが既に日本で予言されていたという驚きのほうが大きかった。」という。
この物語で重要なのは、アインシュタインの相対性理論を超えて自然の解明を数学を駆使した人々の交錯であり、松尾のテーマである。こういう問題を、読者にわからせようとやさしく書いたものではなく本質に迫って書いたものを読むことこそ大事だと思う。そういう意味で松尾の『電子立国日本を育てた男』は勧められる。復刊を求める人が多いが絶版状態であるので、読者には古書市場から入手してほしい。本書は、東北大での抜山平一との対決の場面も豊富であり2段組475ページを超える。できれば松尾に期待したいのだが、ノンフィクションの標準スタイルで写真や資料を添えて八木・湯川・朝永に的を絞って書き直してほしい。
八木は1936年に兼務が解かれて東北大学への影響力を完全に失う。湯川と朝永のディスカッションがされたグランドは、八木が工学部と理学部を往来したときに歩いていたところではあるまいか。1933年にはまだ八木の雰囲気は十分に残っていたと思う。そこにはさまざまの発明発見の場ができた。量子力学では、場は量子と並存する。発明・発見の場の量子は人である。湯川と朝永がちょうど陽子と中性子のようにいたとすれば中間子は誰だっただろうか?
湯川はみずからのペンで八木のことを書き残していない。湯川がノーベル賞を授与された当時、八木は戦時研究の咎による公職追放の身だった。八木は謹んでいたのか自分の関与など発言をしていない。
筆者は、恩師成瀬政男先生(東北大学精密工学科教授の後、職業訓練大学校校長)からは、戦後の八木と湯川の人間関係のことを聞いていた。学術関係者の会議などで湯川は八木には尊敬と畏敬の念を抱いていたようである。もしあのとき八木の苦言がなく、今日ように挨拶としての激励の言葉が強調されていたら、湯川理論の完成は遅れたかもしれない。そうすればきっとヨーロッパの誰かに先んじられていただろう。
囲碁・将棋の世界の指導者は、アマチュアやお客さんは褒めるが、プロの棋士を目指す見込みのある者は絶対に褒めないという。
作家松尾が言うように、八木の最大の業績は湯川にノーベル賞を獲らせたことかもしない。湯川と朝永の東北大学のグランドのディスカッションは当事者二人がそのご何度も思い返して語ったという。
朝永のその後
戦争によって欧米と情報が遮断されているとき、湯川を中心とする量子力学が深められた。朝永は相対性理論を取り入れて理論を発展させて繰り込み理論というものを作っていた。それは量子力学の計算を進めていくと、有限値であるべき物理量が無限大になってしまうことをかなり高い精度で解決する理論のことで、英語ではrenormalization theoryと呼ばれている。このことをイギリスに生まれてアメリカで活躍したフリーマン・ダイソンが次のように述べている。
"All the papers of Professor Tomonaga and his associates which have yet been published were completed before the end of 1945(6?). The isolation of these Japanese workers has undoubtedly constituted a serious loss to theoretical physics."
(朝永教授とそのグループによって発表された論文は1945年の年末以前に完成していたものだった。日本の研究者が隔離されていたことは理論物理学にとっては深刻な損失だったことは確かだ。)
朝永が繰り込み理論を世界に向けて発表したのは1947年のことだ。ダイソンは文学と数学の両方に才能を備えた物理学者で、朝永と一緒に仕事をしていたファインマンとシュウィンガー3人の理論のつながりを明らかにした。そういうこともあって、この3人が1965年のノーベル物理学賞を受賞したのだが、ダイソンは3人枠から漏れた。
参考資料
[※1] 共立出版[※2] ザルツブルグの学会の質疑応答の部分はp.589に23行で語数では150語ぐらいのもの。p.590にドイツ語を引用しながら英語で短かい解説がある。[※3] [※4] 紀伊国屋書店『 電子立国日本を育てた男 -八木秀次と独創者たち-』松尾 博志 ( 著) 文藝春秋
復刊ドットコム [※5] ">Hideki Yukawa Onthe Interaction of Elementary Particles