第49回　テクスチャを立方体の4面に貼る

前回の第48回「テクスチャに遠近法を適用する－ uvt座標の指定」では水平に回る正方形の平面にテクスチャマッピングした。しかし、その結びで述べたとおり、スクリプトの仕組みとしては、とくに平面にかぎってはいない。そこで今回は、立方体の前後左右4面をビットマップで包み、水平に回してみたい（図1⁠）⁠。

立方体の4面にテクスチャマッピングする

前回の「3次元空間の回転する正方形を2次元平面に透視投影してテクスチャマッピング（完成⁠）⁠」するスクリプト2に手を加える。まず、立方体の8頂点座標を、第44回「ワイヤーフレームの立方体を回す」の「立方体の8頂点の座標を決める」と同じくつぎのように定めよう（第44回図2再掲⁠）⁠。

つぎに、テクスチャにするビットマップは、4面を1枚にして[ライブラリ]に納めておく（図2⁠）⁠。ビットマップに設定する[クラス]は、前回のスクリプト2に合わせてImageとする[1]⁠。ここで、Graphics.drawTriangles()メソッドに第3引数を渡そうとしたとき注意しなければならないのは、uv座標が全部で10点あることだ。uv座標（0, 0）と（0, 1）は、テクスチャが立方体を一周してそれぞれ（1, 0）と（1, 1）にくっつく。しかし、テクスチャとしては、これらのuv座標は区別すべきだ。

Graphics.drawTriangles()メソッドの第3引数が10点なら、第1引数の頂点座標ももちろん数を合わせて10点ないといけない。したがって、頂点番号0および3（第44回図2再掲参照）と同じ3次元空間座標の頂点を、8ならびに9として加える（表1⁠）⁠。

表1　頂点番号と3次元空間座標およびuv座標

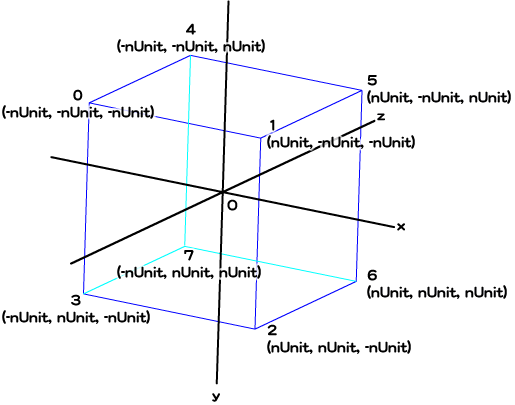
頂点番号	頂点座標	uv座標
0	(-nUnit, -nUnit, -nUnit)	(0, 0)
1	(nUnit, -nUnit, -nUnit)	(1/4, 0)
2	(nUnit, nUnit, -nUnit)	(1/4, 1)
3	(-nUnit, nUnit, -nUnit)	(0, 1)
4	(-nUnit, -nUnit, nUnit)	(3/4, 0)
5	(nUnit, nUnit, nUnit)	(2/4, 0)
6	(nUnit, nUnit, nUnit)	(2/4, 1)
7	(-nUnit, nUnit, nUnit)	(3/4, 1)
8（0と同じ）	(-nUnit, -nUnit, -nUnit)	(1, 0)
9（3と同じ）	(-nUnit, nUnit, -nUnit)	(1, 1)

それでは前回のスクリプト2を書替えよう。基本的には、Graphics.drawTriangles()メソッドに渡す3つのVectorオブジェクトのエレメントを差替えれば、作業は9割方終わる。それが以下のスクリプト1だ。3つのVectorオブジェクト（verticesとindicesおよびuvtData）に、前述立方体の数値を加えている。

スクリプト1　3次元空間で回転させる立方体の4面にテクスチャマッピング（暫定）

// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
// Graphics.drawTriangles()メソッドに渡す3引数のVectorオブジェクトを設定
vertices.push(-nUnit, -nUnit, -nUnit);   // 頂点0
vertices.push(nUnit, -nUnit, -nUnit);   // 頂点1
vertices.push(nUnit, nUnit, -nUnit);   // 頂点2
vertices.push(-nUnit, nUnit, -nUnit);   // 頂点3
vertices.push(-nUnit, -nUnit, nUnit);   // 頂点4
vertices.push(nUnit, -nUnit, nUnit);   // 頂点5
vertices.push(nUnit, nUnit, nUnit);   // 頂点6
vertices.push(-nUnit, nUnit, nUnit);   // 頂点7
vertices.push(-nUnit, -nUnit, -nUnit);   // 頂点8
vertices.push(-nUnit, nUnit, -nUnit);   // 頂点9
addRectangleIndices(0, 1, 2, 3);
addRectangleIndices(1, 5, 6, 2);
addRectangleIndices(5, 4, 7, 6);
addRectangleIndices(4, 8, 9, 7);
uvtData.push(0, 0, 0);   // 頂点0
uvtData.push(1/4, 0, 0);   // 頂点1
uvtData.push(1/4, 1, 0);   // 頂点2
uvtData.push(0, 1, 0);   // 頂点3
uvtData.push(3/4, 0, 0);   // 頂点4
uvtData.push(2/4, 0, 0);   // 頂点5
uvtData.push(2/4, 1, 0);   // 頂点6
uvtData.push(3/4, 1, 0);   // 頂点7
uvtData.push(1, 0, 0);   // 頂点8
uvtData.push(1, 1, 0);   // 頂点9
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
  var nRotationY:Number = mySprite.mouseX * nDeceleration;
  var vertices2D:Vector.<Number> = new Vector.<Number>();
  xTransform(vertices2D, nRotationY);
  xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
  worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
  var myMatrix3D:Matrix3D = worldMatrix3D.clone();
  myMatrix3D.append(viewMatrix3D);
  Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
  myGraphics.clear();
  myGraphics.beginBitmapFill(myTexture);
  myGraphics.drawTriangles(vertices2D, indices, uvtData);
  myGraphics.endFill();
}
// 四角形の4頂点番号をふたつの三角形の頂点番号の組に分けてVectorオブジェクトに納める
function addRectangleIndices(n0:uint, n1:uint, n2:uint, n3:uint):void {
  indices.push(n0, n1, n3);
  indices.push(n1, n2, n3);
}

Graphics.drawTriangles()メソッドに渡す第2引数の3頂点番号の組は、正方形4面なので三角形が8つになる。しかし、立方体は四角形を単位で捉えた方がわかりやすい。そこで、関数（addRectangleIndices()）を定めた。四角形の4頂点番号を引数に渡せば、第2引数のVectorオブジェクト（indices）にふたつの三角形として値を納めてくれる。なお、本連載では3頂点番号の順序は時計回りに決めた（第46回「分割した三角形にビットマップを変形して塗る」「⁠三角形の頂点の組を定める－ Graphics.drawTriangles()メソッドの第2引数」参照⁠）⁠。したがって、関数に渡す四角形の4頂点番号も時計回りとする。

さて、作業は「9割方」終わったといった。それに、スクリプト1のタイトルには、おなじみ「暫定」の文字がある。何が足りないのか。［⁠ムービープレビュー］で確かめてみよう。4面の重ね順が立方体を回しても変わらないのだ（図3⁠）⁠。

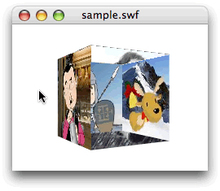
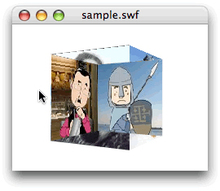
面の裏表の一方だけを描く―カリング

3次元空間における面の重ね順については、第38回「z座標値に応じて重ね順を変える」でも考えた。もっとも、今回4面を描くインスタンス（mySprite）そのものはひとつなので、塗りの順序という方が正確だろう。塗る順番は、Graphics.drawTriangles()メソッドに渡す第2引数（indices）の3頂点番号の組で定まる。後の三角形が上塗りされる。

では、第38回と同じく「z座標値に応じて重ね順を変える⁠」⁠、つまりGraphics.drawTriangles()メソッド第2引数のVectorエレメントに納める頂点番号の順序を換えればよいか。そういう手もある。しかし、今回はGraphics.drawTriangles()メソッドの第4引数を紹介したい。

前掲スクリプト1は、立方体が水平にのみ回る。そのため、見える面は多くてふたつだ。逆にいうと、後ろ側の裏返った面は消してしまってよい。そうすれば、重ね順を気にしなくてもよくなる。このように面の裏表の一方だけを描く処理は「カリング」と呼ばれる。描画が減らせる分、速さも稼げる。Graphics.drawTriangles()メソッドの第4引数は、TriangleCullingクラスの定数によりカリングを指定する。

カリングを決めるには、まず面の向きを確かめる。塗る三角形の頂点番号の順序の方向に右ネジを回すと捉えたとき、ネジの進む向きが面の正方向となる。つまり、頂点番号を時計回りに定めれば、z軸と同じ奥向きが面の正方向だ（表2⁠）⁠。それに対して、今回のスクリプトで見せたいのは、手前に向いた面になる。つまり、負の側の面を描くと定めればよい。定数はTriangleCulling.NEGATIVEだ。

表2　TriangleCullingクラスのカリングを指定する定数

描画する面	TriangleCullingクラスの定数	時計回りの頂点番号で描画される面
正負両面	NONE(デフォルト)	両面
負の方向の面	NEGATIVE	手前向きの面
正の方向の面	POSITIVE	奥向きの面

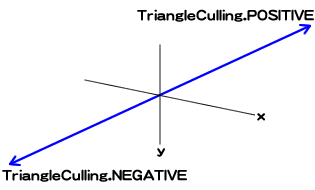
スクリプト1にGraphics.drawTriangles()メソッドの第4引数を加えれば、取りあえず今回のテーマは完成だ。わずか1箇所の追加とはいえ、できあがりなのでスクリプト2として全文を掲げる。カリングで奥向きの裏返った面は消えるため、塗りの順序を変えなくても手前向きの面だけが表示される（図4⁠）⁠。

スクリプト2　3次元空間で回転させる立方体の4面にテクスチャマッピング（完成）

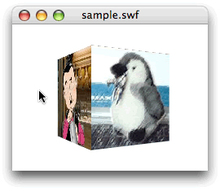
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(nUnit, -nUnit, -nUnit);
vertices.push(nUnit, nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
vertices.push(-nUnit, -nUnit, nUnit);
vertices.push(nUnit, -nUnit, nUnit);
vertices.push(nUnit, nUnit, nUnit);
vertices.push(-nUnit, nUnit, nUnit);
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
addRectangleIndices(0, 1, 2, 3);
addRectangleIndices(1, 5, 6, 2);
addRectangleIndices(5, 4, 7, 6);
addRectangleIndices(4, 8, 9, 7);
uvtData.push(0, 0, 0);
uvtData.push(1/4, 0, 0);
uvtData.push(1/4, 1, 0);
uvtData.push(0, 1, 0);
uvtData.push(3/4, 0, 0);
uvtData.push(2/4, 0, 0);
uvtData.push(2/4, 1, 0);
uvtData.push(3/4, 1, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
  var nRotationY:Number = mySprite.mouseX * nDeceleration;
  var vertices2D:Vector.<Number> = new Vector.<Number>();
  xTransform(vertices2D, nRotationY);
  xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
  worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
  var myMatrix3D:Matrix3D = worldMatrix3D.clone();
  myMatrix3D.append(viewMatrix3D);
  Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
  myGraphics.clear();
  myGraphics.beginBitmapFill(myTexture);
  // myGraphics.drawTriangles(vertices2D, indices, uvtData);
  myGraphics.drawTriangles(vertices2D, indices, uvtData, TriangleCulling.NEGATIVE);
  myGraphics.endFill();
}
function addRectangleIndices(n0:uint, n1:uint, n2:uint, n3:uint):void {
  indices.push(n0, n1, n3);
  indices.push(n1, n2, n3);
}

次回はこのスクリプト2に垂直の回転を加える。そうなると、後ろ側の裏返った面も消してしまう訳にはいかない。つまり、カリングで済ませることはできず[2]⁠、塗りの順序を変えようということだ。

今回解説した次のサンプルファイルがダウンロードできます。

スクリプト2のサンプルファイル（CS5形式/約115KB）