前回の第49回
しかし、
面の塗り順をどのようにして決めるか
立方体の4面を上下左右に回すムービーは、

第38回は4面の中央をx軸またはy軸が貫くように定め、

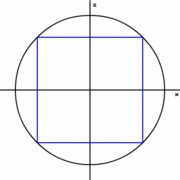
前回のスクリプトでも、
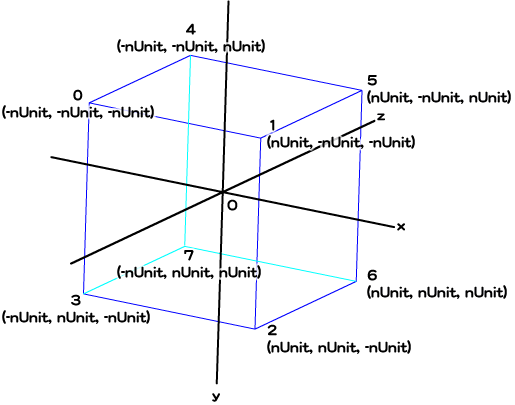
4つの面と中心座標のデータをスクリプトに加える
今回カリングは使えないので、
| 面の位置 | 面の4頂点 | 中心座標 |
|---|---|---|
| 前面 | 0-1-2-3 | (0, 0, -nUnit) |
| 右面 | 1-5-6-2 | (nUnit, 0, 0) |
| 後面 | 5-4-7-6 | (0, 0, nUnit) |
| 左面 | 4-0-3-7 | (-nUnit, 0, 0) |
なお、
まず、
// 4つの面とその中心座標を納めるVectorオブジェクトの初期化
var faces:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
var centers:Vector.<Vector3D> = new Vector.<Vector3D>();
faces.push(new <uint>[0, 1, 2, 3]); // 前面
faces.push(new <uint>[1, 5, 6, 2]); // 右面
faces.push(new <uint>[5, 4, 7, 6]); // 後面
faces.push(new <uint>[4, 8, 9, 7]); // 左面
centers.push(new Vector3D(0, 0, -nUnit)); // 前面
centers.push(new Vector3D(nUnit, 0, 0)); // 右面
centers.push(new Vector3D(0, 0, nUnit)); // 後面
centers.push(new Vector3D(-nUnit, 0, 0)); // 前面4面の頂点番号は変数
var nFaces:uint = 4;
/*
addRectangleIndices(0, 1, 2, 3);
addRectangleIndices(1, 5, 6, 2);
addRectangleIndices(5, 4, 7, 6);
addRectangleIndices(4, 8, 9, 7);
*/
for (var i:uint = 0; i < nFaces; i++) {
addRectangleIndices(faces[i]);
}// function addRectangleIndices(n0:uint, n1:uint, n2:uint, n3:uint):void {
function addRectangleIndices(face:Vector.<uint>):void {
// indices.push(n0, n1, n3);
indices.push(face[0], face[1], face[3]);
// indices.push(n1, n2, n3);
indices.push(face[1], face[2], face[3]);
}ここまでは組み入れた新たな変数に合わせて修正を加えただけなので、
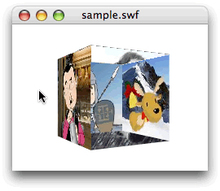
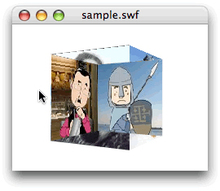
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
// 4つの面とその中心座標を納めるVectorオブジェクトの初期設定
var nFaces:uint = 4;
var faces:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
var centers:Vector.<Vector3D> = new Vector.<Vector3D>();
faces.push(new <uint>[0, 1, 2, 3]); // 前面
faces.push(new <uint>[1, 5, 6, 2]); // 右面
faces.push(new <uint>[5, 4, 7, 6]); // 後面
faces.push(new <uint>[4, 8, 9, 7]); // 左面
centers.push(new Vector3D(0, 0, -nUnit)); // 前面
centers.push(new Vector3D(nUnit, 0, 0)); // 右面
centers.push(new Vector3D(0, 0, nUnit)); // 後面
centers.push(new Vector3D(-nUnit, 0, 0)); // 前面
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(nUnit, -nUnit, -nUnit);
vertices.push(nUnit, nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
vertices.push(-nUnit, -nUnit, nUnit);
vertices.push(nUnit, -nUnit, nUnit);
vertices.push(nUnit, nUnit, nUnit);
vertices.push(-nUnit, nUnit, nUnit);
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
// 三角形の頂点番号の組をVectorオブジェクトに加える
for (var i:uint = 0; i < nFaces; i++) {
addRectangleIndices(faces[i]);
}
uvtData.push(0, 0, 0);
uvtData.push(1/4, 0, 0);
uvtData.push(1/4, 1, 0);
uvtData.push(0, 1, 0);
uvtData.push(3/4, 0, 0);
uvtData.push(2/4, 0, 0);
uvtData.push(2/4, 1, 0);
uvtData.push(3/4, 1, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}
// 四角形の頂点番号からふたつの三角形の頂点番号の組に置換える関数の引数変更
function addRectangleIndices(face:Vector.<uint>):void {
indices.push(face[0], face[1], face[3]);
indices.push(face[1], face[2], face[3]);
}4つの面の塗り順を並べ替える
さて、
改めて確認しておきたいのは、
三角形の頂点番号が納められたVectorオブジェクト
- 4面の中心座標をMatrix3Dオブジェクト
(worldMatrix3D) で変換する。 - 変換された中心座標のzの値により四角形4面の並び順を決める。
- 4面の順にしたがって頂点番号のVectorオブジェクトのエレメントを並べ替える。
考えどころは上述2.だ。中心座標と四角形の4面は、
今回は面の数も少ないので、
function xSetOrder():void {
var transformedFaces:Vector.<Array> = new Vector.<Array>();
for (var i:uint = 0; i < nFaces; i++) {
var transformedVector3D:Vector3D = worldMatrix3D.transformVector(centers[i]);
transformedFaces[i] = [transformedVector3D, faces[i]];
}
transformedFaces.sort(compare);
indices.length = 0;
for (var j:uint = 0; j < nFaces; j++) {
addRectangleIndices(transformedFaces[j][1]);
}
}
function compare(a:Array, b:Array):Number {
var nA:Number = a[0].z;
var nB:Number = b[0].z;
if (nA < nB) {
return 1;
} else if (nA > nB) {
return -1;
} else {
return 0;
}
}まず、
つぎに、
そして、
これで、
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
xSetOrder(); // 追加
xDraw(vertices2D);
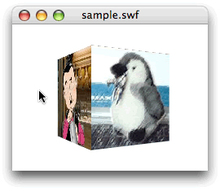
}

// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
var nFaces:uint = 4;
var faces:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
var centers:Vector.<Vector3D> = new Vector.<Vector3D>();
faces.push(new <uint>[0, 1, 2, 3]);
faces.push(new <uint>[1, 5, 6, 2]);
faces.push(new <uint>[5, 4, 7, 6]);
faces.push(new <uint>[4, 8, 9, 7]);
centers.push(new Vector3D(0, 0, -nUnit));
centers.push(new Vector3D(nUnit, 0, 0));
centers.push(new Vector3D(0, 0, nUnit));
centers.push(new Vector3D(-nUnit, 0, 0));
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(nUnit, -nUnit, -nUnit);
vertices.push(nUnit, nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
vertices.push(-nUnit, -nUnit, nUnit);
vertices.push(nUnit, -nUnit, nUnit);
vertices.push(nUnit, nUnit, nUnit);
vertices.push(-nUnit, nUnit, nUnit);
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
for (var i:uint = 0; i < nFaces; i++) {
addRectangleIndices(faces[i]);
}
uvtData.push(0, 0, 0);
uvtData.push(1/4, 0, 0);
uvtData.push(1/4, 1, 0);
uvtData.push(0, 1, 0);
uvtData.push(3/4, 0, 0);
uvtData.push(2/4, 0, 0);
uvtData.push(2/4, 1, 0);
uvtData.push(3/4, 1, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
xSetOrder(); // 追加
xDraw(vertices2D);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}
function addRectangleIndices(face:Vector.<uint>):void {
indices.push(face[0], face[1], face[3]);
indices.push(face[1], face[2], face[3]);
}
// 頂点番号で定める面の順序を並べ替える
function xSetOrder():void {
var transformedFaces:Vector.<Array> = new Vector.<Array>();
for (var i:uint = 0; i < nFaces; i++) {
var transformedVector3D:Vector3D = worldMatrix3D.transformVector(centers[i]);
transformedFaces[i] = [transformedVector3D, faces[i]];
}
transformedFaces.sort(compare);
indices.length = 0;
for (var j:uint = 0; j < nFaces; j++) {
addRectangleIndices(transformedFaces[j][1]);
}
}
function compare(a:Array, b:Array):Number {
var nA:Number = a[0].z;
var nB:Number = b[0].z;
if (nA < nB) {
return 1;
} else if (nA > nB) {
return -1;
} else {
return 0;
}
}立方体を上下左右に回す
ここまでくれば、
第1は、
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
var nFaces:uint = 4;
var faces:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
var centers:Vector.<Vector3D> = new Vector.<Vector3D>();
faces.push(new <uint>[0, 1, 2, 3]);
faces.push(new <uint>[1, 5, 6, 2]);
faces.push(new <uint>[5, 4, 7, 6]);
faces.push(new <uint>[4, 8, 9, 7]);
centers.push(new Vector3D(0, 0, -nUnit));
centers.push(new Vector3D(nUnit, 0, 0));
centers.push(new Vector3D(0, 0, nUnit));
centers.push(new Vector3D(-nUnit, 0, 0));
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(nUnit, -nUnit, -nUnit);
vertices.push(nUnit, nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
vertices.push(-nUnit, -nUnit, nUnit);
vertices.push(nUnit, -nUnit, nUnit);
vertices.push(nUnit, nUnit, nUnit);
vertices.push(-nUnit, nUnit, nUnit);
vertices.push(-nUnit, -nUnit, -nUnit);
vertices.push(-nUnit, nUnit, -nUnit);
for (var i:uint = 0; i < nFaces; i++) {
addRectangleIndices(faces[i]);
}
uvtData.push(0, 0, 0);
uvtData.push(1/4, 0, 0);
uvtData.push(1/4, 1, 0);
uvtData.push(0, 1, 0);
uvtData.push(3/4, 0, 0);
uvtData.push(2/4, 0, 0);
uvtData.push(2/4, 1, 0);
uvtData.push(3/4, 1, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var nRotationX:Number = mySprite.mouseY * nDeceleration; // 追加
var vertices2D:Vector.<Number> = new Vector.<Number>();
// xTransform(vertices2D, nRotationY);
xTransform(vertices2D, nRotationY, nRotationX);
xSetOrder();
xDraw(vertices2D);
}
// function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
function xTransform(vertices2D:Vector.<Number>, myRotationY:Number, myRotationX:Number):void {
// worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
worldMatrix3D.appendRotation(myRotationY, Vector3D.Y_AXIS);
worldMatrix3D.appendRotation(myRotationX, Vector3D.X_AXIS); // 追加
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>):void {
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}
function addRectangleIndices(face:Vector.<uint>):void {
indices.push(face[0], face[1], face[3]);
indices.push(face[1], face[2], face[3]);
}
function xSetOrder():void {
var transformedFaces:Vector.<Array> = new Vector.<Array>();
for (var i:uint = 0; i < nFaces; i++) {
var transformedVector3D:Vector3D = worldMatrix3D.transformVector(centers[i]);
transformedFaces[i] = [transformedVector3D, faces[i]];
}
transformedFaces.sort(compare);
indices.length = 0;
for (var j:uint = 0; j < nFaces; j++) {
addRectangleIndices(transformedFaces[j][1]);
}
}
function compare(a:Array, b:Array):Number {
var nA:Number = a[0].z;
var nB:Number = b[0].z;
if (nA < nB) {
return 1;
} else if (nA > nB) {
return -1;
} else {
return 0;
}
}[ムービープレビュー]を確かめると、
第1に、

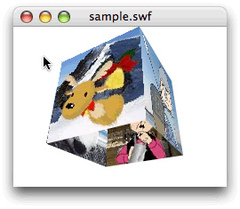
テクスチャマッピングは今回で終える。次回は3次元空間座標を回転するMatrix3Dクラスのメソッドについて、



