「ピタゴラスの定理でわかる相対性理論」を佐野茂氏と著し、補講をしてまいりました。最初は本書に盛り込めなった公式の証明を取り上げ、いろいろな話題に触れてきました。そして、第10回 では E=mc2 論文の全訳からから新しい展開をしてまいりました。さらに、これとE=hv との関係を語った後に日本の素粒子研究や電子工学の発展に入りました。
前回 は「ライバルの対話」という発想で、アインシュタインとハーゼンエールおよび湯川と朝永をテーマにしてみました。今回は最終回として、昨年のノーベル物理学賞を引用しながら宇宙存在の理由と、ささやかながら地球環境保全の問題に触れたいと思います。
1.次々と見つかった素粒子と宇宙存在の理由
湯川秀樹の中間子論がきっかけとなって素粒子という言葉ができて、素粒子論という分野が生まれ急速に発展しました。素粒子とは、「 物質を細分化していって最後にたどりつく究極の粒子」のことですが、これが複雑な様相を示すようになりました。それは加速器の進歩があって、その成果としてさまざまな粒子が見つかったからです。加速器では電子や陽電子を光の速度に近い速度まで加速して電子核に衝突させて、素粒子を発生させる装置です。素粒子の種類を表1 と表2 にまとめておきます。
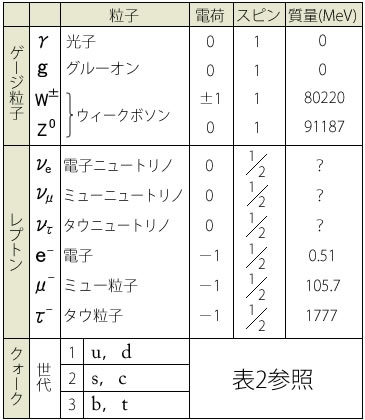
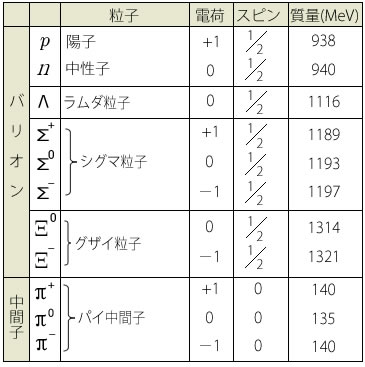
表1 素粒子の種類A:基本粒子
B:ハドロン(複合粒子)
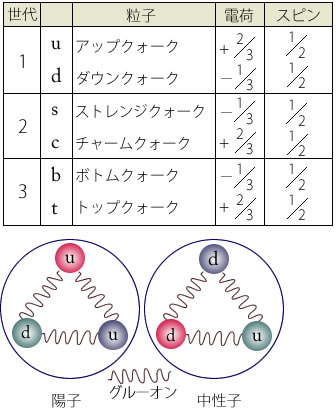
表2 クォークの種類このあたりのことをやさしく書いた本はいろいろありますが、初めての方には、佐藤勝彦著『図解雑学 量子論』[ ※1 ]をお勧めします。さらに詳しくは、Internetで専門家が参照するhttp://pdg.lbl.gov/ があります。
1936年にアンダーソンが宇宙線から電子の質量の200倍ほどの粒子を見つけたとき、それは湯川の予言した中間子だと思われたのですが、実は電子の兄弟分のようなミュー粒子でありレプトンに属します。湯川の中間子はハドロン(複合粒子)に属する π 中間子です。
ハドロンはクォークの複合体と考えられています。1964年にアメリカのゲルマンとツワイクは別々に究極の粒子クォークのモデルを発表しました。
こういうなか、理論物理学の関心はそもそも物質あるいは宇宙が存在する理由― 数学的な説明― ができるかに寄せられたようです。
2008年のノーベル物理学賞は宇宙存在のためのCP対称性の破れに関するもので、南部陽一郎、小林誠、益川俊英の3氏が受賞されたことは周知のことです。受賞理由として正式には次のように言われています。
南部陽一郎 :粒子の質量起源に関する自発的対称性の破れ小林誠・益川俊英 :CP対称性の破れの起源の発見Cはcharge conjugate ( 荷電共役性、正に対する負、電子に対する陽電子のような対称性) 、Pはparity(波動の山と谷に関連するような対称性) 。
前回までに、ディラックが E=mc2 のエネルギー式と運動量を加味して、さらにシュレディンガーの波動方程式を統合して、陽電子の可能性を指摘したことに触れました。陽電子とは正電荷をもった電子 ― つまり反電子です。ビッグバンによって宇宙が発生したときに物質(さまざまな粒子) と反物質(反粒子)ができて、反物質はほとんど消滅して物質が残って現在の宇宙があるとする考えがあります。粒子に対する反粒子の関係は一つの対称性です。この対称性にわずかの乱れが発生することが素粒子の質量の起源だというが南部の理論です。
CP対称性あるいはCP保存則とは、
「粒子と反粒子を入れ替えた世界の物理法則が、ちょうどわれわれの世界を鏡で見たとき(時空反転)と同じになっているばずだ。」という命題です。
ところが1964年に、わずかにCP保存則が破れている現象が発見されました。当時はそれを説明する理論がありませんでした。このときにはクォークとして「アップ」 、「 ダウン」および「ストレンジ」の3つが発見されていました。そこに、4組(カルテット)で完全になるので残る一つ(チャームクォーク)見つかるだろうという説が出ていました。しかし1972年寄稿・翌年刊行小林・益川の論文[※2 ]は、カルテットでは対称性が破れないことを指摘し、対称性が破れる可能性として、6種類のクォークモデルを示唆しました。それは複素数の導入に深く関係する理論です。表1,2には第1世代、第2世代、第3世代として6個のクォークが示されています。
小林・益川論文の概要[※2] In a framework of the renomarizable theory of week interaction, problems of CP-violation are studied. It is concluded that no realistic models of CP-violation exist in the quartet scheme without introducing any other new fields. Some possible models of CP-violation are also discussed.
弱い相互作用の繰り込み理論の枠内でCP-対称性の破れを検討したところ, 4組構造では何か新しい場を導入しないかぎり対称性の破れが起きそうな現実的なモデルがないことがわかった。さらにここでCP対称性の破れの可能性あるモデルをいくつか検討する。
ガウスの複素平面は2次元です。2次元は複素数になじみやすいのですが、3次元空間に複素数を持ち込むと数学ではうまくいかないとされています。小林・益川の理論はこういう意味の3次元空間とは違って、現実のクォークと純粋なクォークの3世代間の混合に関する数学表現を提示したものです。各世代に2個のクォークをあてて、ここに混合比として複素数を持ちこむと、位相回転で吸収しきれない複素位相が残り、これがCP対称性の破れにつながるとするものです。
1974年にチャーム、1977年にボトムクォーク、1995年にトップクォークが発見され現在は6個のクォークが見つかっていることになります。CP対称性の破れの理論の実験による検証は、2001年に筑波の高エネルギー研究所の加速器で成功しました。
これは蛇足かと思うのですが、小林・益川の論文は必要なことだけをさりげなく書き上げて、余計な謝辞もない点でアインシュタインの論文と通じるものがあり、読者の心を癒します。
ちなみに2002年のノーベル物理学賞の一人が小柴昌俊氏で、ニュートリノ天文学を創始し開拓した業績に対するものでした。表1にあるように、ニュートリノの名のつく素粒子は3個あります。
現在の有力な説では:物質のすべては6種類のクォークと6種類のレプトンで構成されているといわれています。3つのクォークで中性子あるいは陽子ができて、電子はレプトンの1種とみなされています。
しかし宇宙の起源についてはまだ謎が多くて、南部先生の理論[※3 ]ではまだ全宇宙の質量の起源は説明できないと言われています。
アインシュタインの奇跡1905年の論文から100年あまりの今、宇宙と物質と光の根源の追究が最後の一押しのところに来ているのでしょうか?
2.本書の意義を箇条書きにしてみます。
最終回ということで、『 ピタゴラスの定理でわかる相対性理論』の意義を考察してみたいと思います。
(1)特殊相対性理論と非ユークリッド幾何の結びつけ
相対性理論のほとんどというよりすべての本が、特殊相対性理論のあとで一般相対性理論と非ユークリッド幾何とを結びつけています。つまり、重力とは空間の曲がりであるとする理論ですが、そこで初めてリーマンの非ユークリッド幾何が登場します。たしかに、アインシュタインがクラスメートでETHの数学の教授になっていたグロスマンの手ほどきでリーマン幾何を勉強したのは1910年ごろからでしたし、相対性理論をさらに発展させて重力の問題をテーマにするときでした。
実は、本書はアインシュタインも気づいていなかった数学を語ったとも言えます。リーマン幾何は双曲幾何だけなくユークリッド幾何も球面幾何も統合した幾何です。特殊相対性理論の時空は双曲幾何空間の典型的な事例だったのです。数学者によって人工的に作られたと思われた非ユークリッド空間が実は宇宙空間だったという物語です。これをまとまった形で語ったのは本書が世界初だと思います。
(2)これをカットなしに高校生の数学レベルの数学で論じきった。
この類の本の著者や編集者は、多くの読者には難しいだろうから数式やその解説をカットして日常用語で無理に語ろうとするために、かえってわかりづらくなります。しっかり語る本が高校生のために必要です。湯川は、第三高等学校時代に、図書館にドイツから送られてくる物理学雑誌を、鼠が餌をかじるように読んでいたということです。そのうちに量子力学の発展のために自分の出番がなくなってしまうのではないかと不安でならなかったとも書いています。今だってそういう高校生がいるはずです。そういう若人に満足していただける本がなくてはいけないと思います。
3.ではこの補講の意味は?
そこであらためてこの補講の意義を考えてみると、2つあったように思います。
(1)アインシュタインの物理学が1905年26歳で開花した物語
これは相対性理論と量子力学を同時に誕生させた論文の共通点に関することでもあります。アインシュタインの論文の評価がしだいに高まり、彼はやがて名声を得て母校の助教授、プラハのドイツ大学、そしてまた母校の教授、さらにベルリン大学教授と出世するのですが、名声とか有名というものが人格形成にとって、たいていは危険です。本書は16歳の少年から青年に入り有名になる前の10年間のアインシュタインがどんなことを考えたのかに的を絞ろうとしました。
(2)数学から物理学へ
本書は数学の本でした。 E=mc2 からは物理学の世界に入るので、そこで本書は終了したのですが、やはり数学の次に物理を考えながらこの式について詳しく語る必要があると判断して、この補講(第10 、12 、14 と15回 )で語ってきました。
第13回 では、相対性理論でのエネルギーと運動量の関係から、量子力学のシュレディンガーの波動方程式を導きました。そして電磁波と物質波の違いを明らかにしました。これは第6回 の「光と電磁波」を補完するものです。
(3)奇跡の1905年後から日本の時代までの展望
アインシュタイン、プランク、ハイゼンベルグ、シュレディンガーの系譜によって量子力学が完成しました。それを日本に持ち込んだのが仁科芳雄です。それが2008年のノーベル物理学賞に関係する「宇宙存在の理由」の解明につながった物語を手短に紹介しました。
宇宙が存在するなかで、本書 p.214にも書いたようにこの地球は奇跡の惑星です。ここに多くの生命が私ども人類ともに棲息しています。理論物理学によって宇宙が存在する根拠が明らかにされていることはひとつの見識かもしれません。しかし宇宙の中の奇跡の惑星である地球を存続させる知恵は理論物理学だけでは得られません。さまざまの科学の知恵はもちろんですし、工学も重要かもしれません。これは次のテーマです。
4.天職(Calling)と見城の役割
本書の執筆中に英語の資料をよく調査してくださった武口隆という人がいます。私から見ると武口さんは、日本語から英語への翻訳あるいは学術英文推敲のプロというより、彼の天職が英作文のように思えるのです。豊富な語彙の中から最も適切な1語を選び出す凄さは抜群です。武口さんと26歳当時のアインシュタインのことをディスカスしていて、物理の理論創出こそアインシュタインのcallingだという考えで一致しました。ここでいうcallingは電話をかけることではありません。神の召命つまり天職です。神は、スイスの特許局に勤務するある技師を魂の世界にお呼びになり新しい物理の創出を彼の仕事とお定めになった、と解釈しましょうか。
アインシュタインはモーツアルトやガウスのように神童だったのではなかったようです。このことがいかにもcallingだと感じます。
筆者はなぜアインシュタインのことを書いているのか不思議です。相対性理論や量子力学を専門とする物理学者ではありません。このことを天職ということばで釈明しておきたいと思います。先にも書いたように、大学の1~2年生の物理は何とか理解できて6回の定期試験も悪くはなかったと思います。しかし専攻を電子工学と決めたのに、電子物理の理解度は低いなと感じました。アインシュタインとの距離がものすごく大きいと実感したのです。大学院に進んでプラズマ工学とはいうものの実際にはプラズマ物理の勉強を始めて、理学部の相対性理論や量子力学の単位を取ろうと思って授業には出てみました。しかし、なかなか理解できるものではありませんでした。ローレンツ変換のいう時空の関係などは頭にしっかり入らないうちに講義はどんどん進んでいってしまいました。
その一方で、3年生の工学部の講義のなかでピンと感じるものがいくつかあったのです。一つは機械工学通論です。成瀬政男教授の名講義を聞いていて、自分の仕事はメカトロニクスだと閃いたのです。まだ当時そんなコトバはありませんでしたが、ヒントがありました。量子力学から発達した光の技術が当時オプトロニックスと呼ばれていたように思うのです。本来ならopto-electronicsですが短縮されてoptronicsといわれていたような記憶が残っています。自分は機械と電子の技術を結びつけてみよう、と考えたのです。そして浮かんだ言葉がメカトロニクス(mechatronics)です。
もう一つ、電子工学科でありながら電気工学科の伝統科目であるモータや発電機をテーマとする電気機械が必修科目でした。少年のころに模型電気機関車のモータいじりが好きだからといって、学問としてのモータ理論を講義で理解するのはやさしくはありません。何を聞いているのかわかりません。
ところが、主要なモータと発電機に関する講義が終わって、特殊モータの一つでヒステリシスモータの話を5分ほど聞いたときのことですが、不思議なことに鮮明に理解できて、しかも感激まで感じたのです。そして3年後に本当に偶然に最初の仕事としてヒステリシスモータの改良設計をすることになったのです。運命に導かれているようで、天職かなと思いました。それ以来、さまざまの種類の小形モータの研究とそれをアナログ・デジタルの電子機器で制御する技術-メカトロニクス-を発展させるようになったのも事実です。
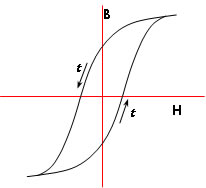
ヒステリシスとは磁性に関する現象で、普通は図1 のように、強磁性体に起きる磁界強度と磁束密度の関係で説明されます。磁束密度 B の時間的な変化は電流で作られる磁界強度 H の変化よりも時間的に遅れるという現象です。それは磁性体の一部だけをみたときの現象です。この研究のイニシャティブをとりhysteresisというコトバを作ったのは、1878年に若くして東大教授として招聘されたJames Alfred Ewing(ユーイング)です。
図1 ヒステリシスところが、この時間的な変化が空間的な広がりをもって起きるとき、各所の時間的な関係をうまく制御すると推力や回転力が発生するのですが、その原理というか理由を即座に理解できたのです。推力や回転力は、方向があることから分かるように空間的な現象です。時間的現象と空間的な作用の関係の一つ応用が、ヒステリシスモータです。このモータの発想の原点はシュタインメッツにあったことや、彼もアインシュタインと同じようにドイツに生まれて、チューリッヒの現在のETHで学んだことを知ったのはずっと後のことでした。このヒステリシスの奥に、時空の本質としてメカトロニクスの基本法則が潜んでいると思うようになりました。筆者がアインシュタインの青年時代の仕事に関心があるのはこのためです。宇宙とか、時空の本質的性質を使って動きを発生するメカニズムこそモータだと思うのです。
モータは現代人になくてはならないツールです。そういう背景で考えるのですが、アインシュタインは電気力学というときモータのことを考えなかったのだろうかという疑問です。考えたと思います。ドイツでもイタリアでも彼の実家は電気機器を製作していました。当時のその代表格が発電機やモータです。またアインシュタインは論文の対象として発電機やモータを取り上げなかったのはなぜでしょうか? 簡単な理由は、すでに最先端ではなかったという答えはあるかもしれないのですが、納得できません。
アインシュタインのような凄い頭脳に、もしや電気力学に関してほかに何かひらめいた形跡がありはしないだろうか? という疑問は筆者の頭にありました。
彼は考えたと思いますが、釣りに喩えると、狙っていたものより大きな魚(量子力学や相対性理論)が獲れてしまったのかもしれません。特殊相対性理論や光電効果の考察の後になったのですが、アインシュタインが電磁力による物体の回転運動について考えたのだという証拠が1915年の英語論文かもしれません。一般相対性理論を完成した年にオランダのDe Haasと実験をした結果を論じているのです。理論物理学者アインシュタインの唯一の実験論文です[※4,5 ] 。
最後に、佐野氏への期待を記したいと思います。宇宙存在の理由についての必読書として勧めたいのが小林誠氏の『消えた反物質』[ ※6 ]です。これを書いたのはノーベル賞受賞の11年前のことですが、最後のところにこんな記述があります。
・・・・現実の自然界がゲージ理論という枠組みの中で記述できるということは大きな発見だったが、あるがままに記述するだけでは自然を本質的に理解したことにはならない。どんなゲージ群のもとで、どれだけの基本粒子が、いかに存在するかを支配する原理が求められているというのである。
宇宙の起源や宇宙が存在する物理的・数学的な説明が完全にはできてはいないようです。物理的にはゲージ理論という枠組みで作られているようですが、時空の数学構造を根底から思索している数学者の参画があったのかどうか筆者(見城)は知りません。見城が佐野茂氏に期待するのはこのあたりです。言い換えると、素粒子あるいは宇宙存在の理由を非ユークリッド幾何と関連させて数学的なヒントを見つけだしてほしいことです。これは佐野氏の天職の一課題かもしれないと思うのです。筆者見城による補講はしばらくお暇をいただき、佐野氏から何か答えが得られたら補講の番外としていただけると期待します。
参考資料
[※1] ナツメ社[※2] 49, No.2, 1973[※3] ( ブルーバックスB1205) 、講談社[※4] Einstein and W.J. de Haas: Experimental proof of the existence of Ampere's monocular currents, Proceedings Royal Academy Amsterdam, Vol.XVIII, pp.696-711[※5] http://www.ptb.de/en/publikationen/jahresberichte/jb2005/nachrdjahres/s23e.html [※6] ( ブルーバックスB1174) 、講談社
コラム サンマルコを望む
上野松坂屋の画廊で、木脇康一作の『サンマルコを望む』に思わず心を惹かれました。サンマルコ聖堂とドカーレ宮殿の背景では緑を帯びた青い海が空の青と溶け合おうとしています。聳え立つ鐘楼のレンガ色も気に入りました。
イギリスの画家ターナー(1775-1851)は44歳のときにベネチアをおとずれ、海の光と空が融合する風景に感激して多くの作品を描いたそうです。この絵を見たとき筆者はターナーの心を捉えた「明るい陽光と色彩」を連想しました。そして、『 ピタゴラスの定理でわかる相対性理論』を書いているときを思い出しました。
それは、ユークリッド幾何から双曲幾何が生まれるときの数学史の一里塚として、複比という概念が現れたときを語った第4章後半です。共著者の佐野茂氏から数学理論をきいて、咀嚼しなおしていくつかのイラストを創作して説明したところであり、イタリアで起きた透視画法(遠近法)の発達と密接に関連します。
古代ギリシャ人が創造した幾何学は、ナイル川周辺を対象とした広い平面であり、やがて紙面で展開されたユークリッド幾何でした。そこでは1本の直線に対して、その上にない点を通る平行線は1本だけ存在するのですが、ユークリッド自身も釈然としない公理でした。後に地球が丸いことが分かったこともあって、平面と想っていたものが球面の一部であることに着目して球面幾何が生まれした。そこでは平行線は一つもありません。しかし謎は未解決でした。ところが、風景を描くための遠近法の理論に現れる複比とガウスが導入した複素平面とを結び付けて、ポアンカレは双曲幾何を提唱しました。そこには平行線は無数にありました。これこそアインシュタインの特殊相対性理論を説明するための宇宙構造の4次元の幾何学だったのです。
第6章に書いたように、オランダの画家エッシャーは透視画法に疑問を感じて、その欠陥をだまし絵として指摘しました。しかし数学者Coxeterに出会って双曲幾何を知り、傑作『極楽と地獄』( p.128)を制作しました。作家がこのような苦難の末にたどり着いた作品をみたときに見る者が感じるのが形容しがたい疲れです。それは図形に対する意図的なトリックのためかもしれません。
一方、単純な図形には無限の奥深さが宿されています。本書の第1章では、寺院の床や壁のタイルを見て宇宙根源の法則を想起できる人はいるだろうかと問いました。
この『サンマルコを望む』からは安らぎを感じます。構図には余計な複雑さを感じません。幾何では直線とは何かが基本問題で、直線の定義は幾何学ごとに違っています。本書p.95に記したように、ユークリッド幾何では第2種合同変換によって不変な点の集まりが直線であるとしたのは、クライン(1845-1925)でした。それを折り紙によって説明しなおしてみました。
この絵では、空からの散乱光と海からの反射光が一致するところが水平線でもあり、一つの直線ともいえそうです。ベネチアは小さな島ですからこの画面の左右を想像します。それは水平線だといってしまうと水平線とは何かを説明するのが厄介です。
宇宙構造の不思議の一つが光速不変の原理であることは『ピタゴラスの定理でわかる相対性理論』で論じました。どんな波長あるいはどんな振動数の光も、秒速30万キロメートルで伝播します。また、対岸のマッジョーレ広場でこの風景を描いている画家にも、モータボートを操縦している人にも光の速度は同じです。アインシュタインは光の生成と吸収についても深く考えて、量子力学を創出したことは補講で解説しました。
私たちにとって重要な光の特質は、可視光による色彩です。この絵の風景に満ちているのは散乱光と反射光です。太陽から降り注ぐ光は空気で散乱して空の色は青くなります。それが海に反射するとき特定の波長が海面に吸収されるので、青緑に見えます。もし光速不変性がなかったら、この風景の色彩はまったく違うものになりそうですし、この美しさもどうなるか分かりません。
地球温暖化が進むと南極の氷が解けてベンチアは水面下に没するといわれています。本書とその補講では宇宙の構造を深く考えてきました。そして昨年のノーベル物理学賞のテーマであった宇宙が存在する理由にも思いを馳せてきたのですが、むしろ大事なのが、本書p.216にも語ったように、知的生命体の繁栄のために地球がかけがえのない存在であることを願うことです。水の都ベネチアを永遠のものとすることは、地球規模での挑戦です。